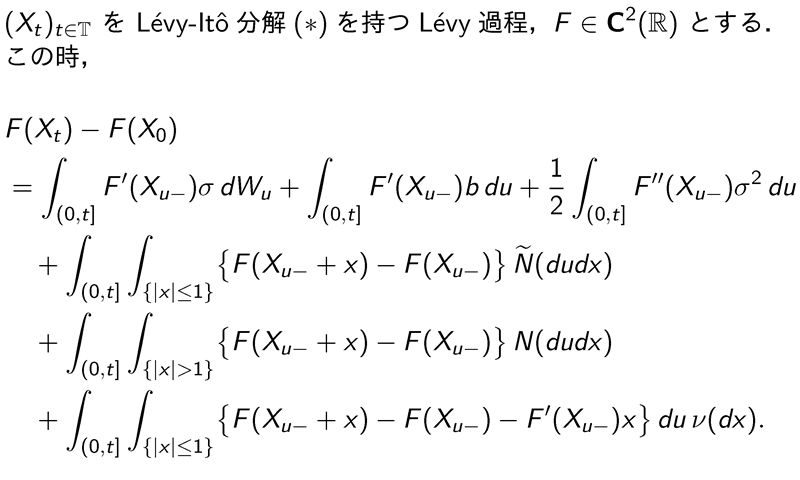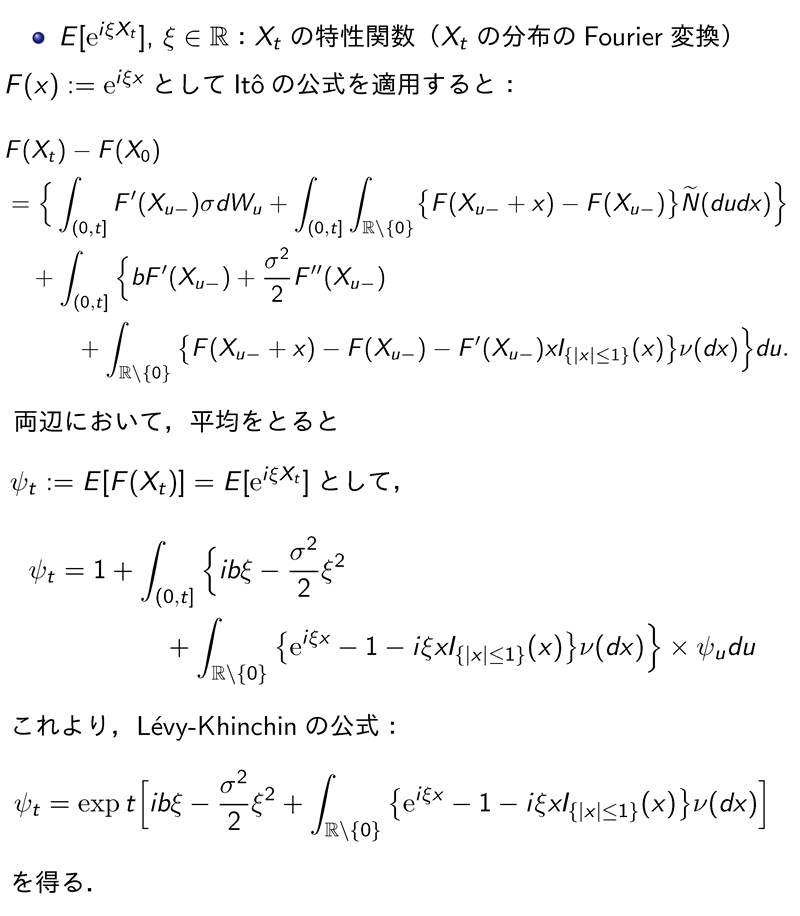研究

これまでの研究内容

Lévy 過程

Lévy-Itô の分解定理から伊藤解析へ

飛躍を持つ確率過程とは：基本としてのLévy 過程

Lévy 過程の例

Lévy-Khinchin の公式(Lévy(1934), Khinchin(1937))

Lévy-Itô の分解定理に向けて：Lévy 過程の誘導する計数測度

Lévy-Itô の分解定理(1942)

Lévy-Khinchin の公式とLévy-Itô の分解定理の比較

Lévy-Itô の分解定理の意味

マルチンゲールの定義

Lévy 過程に対するItô の公式

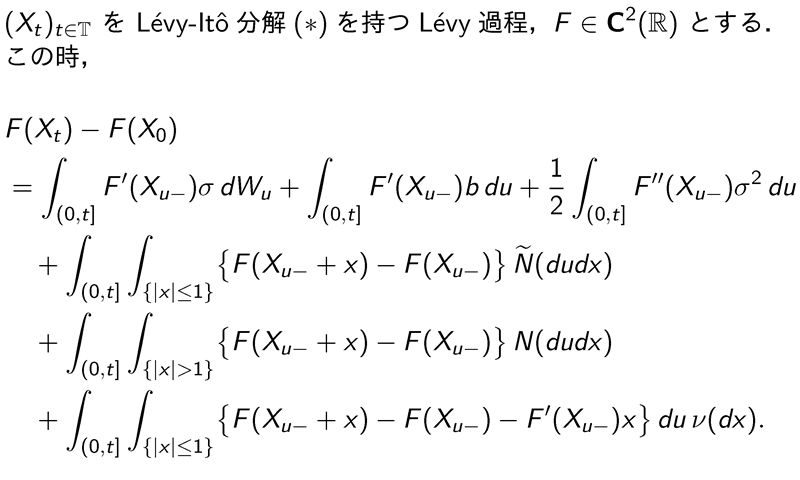
Itô の公式の適用例その１

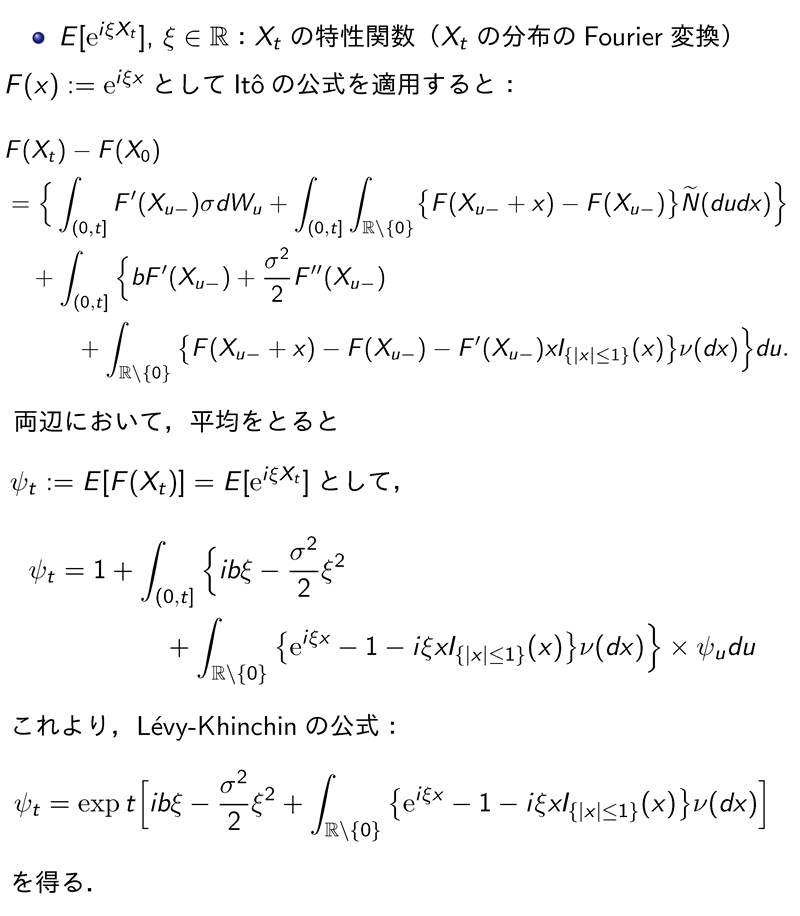
Itô の公式の適用例その2　指数型Lévy 過程

数理ファイナンスとの関わり

数理ファイナンスモデルとしての指数型Lévy 過程：指数型Lévy 過程モデル

1次元Black-Scholesモデル

指数型Lévy 過程モデルでは

そこで[Fujiwara-Miyahara(2003)] では

条件(C)：

[Fujiwara-Miyahara(2003), Theorem 3.1]

資産の指数型効用最大化戦略

[Fujiwara(2006), Theorems 3.1 and 3.2]

指数型Lévy 過程モデルを超えて

これからの研究の方向

論文リスト

stochastic flow

飛躍を持つ確率過程についての極限定理（その１）

飛躍を持つ確率過程についての極限定理（その２）

数理ファイナンス関連（その１）

数理ファイナンス関連（その２）