平面によるトーラスの切断

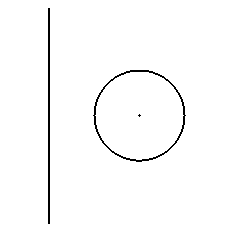
平面上の円と（円と交わらない）直線があるとき， 直線の周りに円を1回転して得られる曲面がトーラス （ドーナツ，浮き輪） である． 直線（回転軸）と円の中心の距離を a，円の半径を b とする． 回転軸を z 軸，円の中心は x 軸上の (a, 0) にあるとして， トーラスのパラメータ表示（媒介変数表示）は， x = (a +b cost )cosu, y = (a +b cost )sinu, z =b sint により与えられる （パラメータ t, u は 0 から 2π まで動く）．

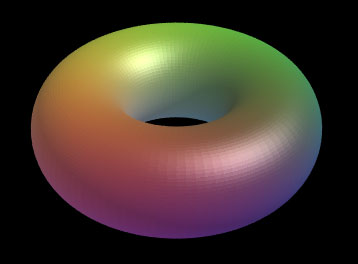
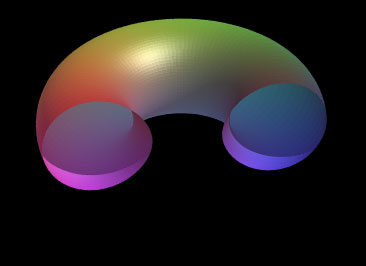
下の一番左の図は a =1, b =1/2 として描いたトーラスの図で， 続く3つの図は回転軸と平行な平面でトーラスを切断した断面図である． 左から3番目の図では，切断面に現れる曲線はレムニスケートである．

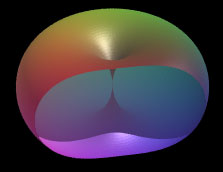
一般の a, b に対しても， 回転軸に平行な切断面と軸との距離が b （回転する円の半径） に等しいとき， トーラスと切断面の交わりはカッシーニの卵形線になる． （トーラスのパラメータ表示と平面 y = -b から t, u を消去して， カッシーニの卵形線の方程式（陰関数表示）が導かれる．） 下の図は， a =1，b =0.4, 0.5, 0.6, 1 の場合にこうして得られるカッシーニの卵形線である．

円錐を平面で切ると2次曲線（放物線，双曲線，楕円）が現れる． 円錐の平面による断面 (conic section) はメナイクモス (BC350)， トーラスの平面による断面 (spiric section) はペルセウス (BC150) によって最初に考えられたそうだ．

以上は [1] の5章「ドーナツの輪切り?」 を読んで， 2001年に作った Maple ワークシートをまとめたものである． plottools パッケージの torus コマンドでトーラスを作り， plots[display] コマンドで描く範囲を制限することにより切断面を作っている． 上の図はMapleプロットを Pov-Ray 形式で保存して Pov-Ray で描画した．以下のような Maple コマンドを用いた．

with(plots):with(plottools):
a := 1: b := 1/2:
t := torus([0,0,0], b, a):
display(t,scaling=constrained, axes=boxed, labels=[x,y,z]);
display(t, view=[-a-b..a+b, -a-b..b, -b..b], scaling=constrained, 
orientation=[80,60]);

1. 山本芳彦 『実験数学入門』岩波書店, 2000.
2. ニーダム 『ヴィジュアル複素解析』培風館, 2002.

（2005年5月31日作成（2009年4月24日 修正して再公開））