カッシーニの卵形線

楕円は平面上の2定点からの距離の和が一定である点の軌跡として定義される．これに対して， 平面上の点 P と2定点 F₁, F₂ との距離の積 F₁P・F₂P が一定であるような点 P の軌跡を カッシーニの卵形線という． 座標平面内で，2定点を F₁(-1, 0), F₂(1, 0), 動点を P(x, y) とすると， 距離の積の2乗は ((x +1)²+y²)((x -1)²+y²) = (x²+y²)²-2x²+2y²+1 に等しい．定数項 1 を除いて f (x, y) = (x²+y²)²-2x²+2y² とおくと，カッシーニの卵形線は2変数関数 f (x, y) の等高線 f (x,y)=C （C は定数）である． 特別な場合として， 2定点からの距離の積が2定点間の距離の半分 （今の場合は 1） になるような平面上の動点の軌跡，f (x, y)=0 をベルヌーイのレムニスケートという． 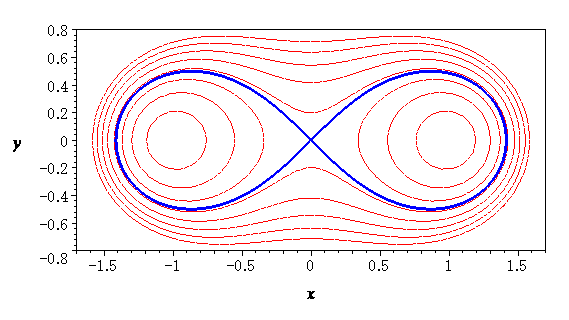いくつかの C の値について，カッシーニの卵形線を描いたのが上の図である． レムニスケートは青線で表している．

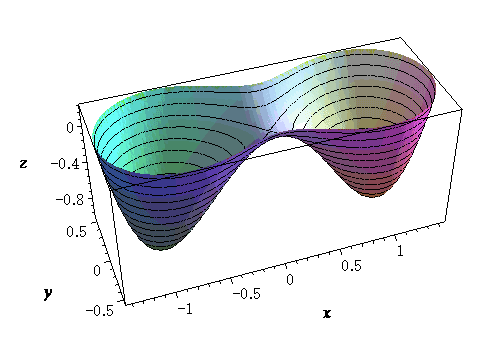
z = f (x, y) のグラフは次のような曲面である． 等高線や曲面の図から f (x, y) は，(-1, 0), (1, 0) で 極小値をとり，(0, 0) は鞍点であることが観察される． 実際にこれらを確かめるのは，2変数関数の微分法の練習問題である （ [2] IV.3.7　3-8, IV.4.3 参照）． カッシーニは惑星の軌道が卵形線であると考えたが， 惑星の軌道は焦点の一方に太陽が位置する楕円であることをニュートンが示した． 楕円は2定点 F₁, F₂ からの距離の「和」 F₁P+ F₂P が一定であるような平面上の点 P の軌跡である （[3] 第2章 II 3節参照）．

上の2つの図は Maple8 を用いて作成した．レムニスケートは 極方程式 r ²=cos 2θ を用いて polarplot コマンドにより描いた． 3次元プロットは次のコマンドで出力した．

plot3d((x^2+y^2)^2-2*x^2+2*y^2,x=-1.5..1.5,y=-1..1,
axes=boxed,view=[-1.46..1.46,-0.57..0.57,-1..0.25],
style=patchcontour,scaling=constrained,projection=0.8,
orientation=[-110,50],grid=[100,100], labels=[x,y,z],
labelfont=[TIMES,ITALIC,14], axesfont=[HELVETICA,12],
lightmodel=light4);