この文章は大学1年生の微分積分の授業の配布プリントとして OpenOffice3.01 で作成したものを html 出力して若干の手を加えたものである.(pdf ファイルはこちら. OpenOffice の数式編集機能を使うのは初めてなので結構大変だった. html 出力すると数式がグレーっぽくなり見にくい.) これに関連して,フリーの数学ソフトウエア Geogebra を用いて, Javaを使ったインタラクティブなテイラー展開のページを作成した (指数関数の例と正弦関数の例). 授業期間が終了しても残しておくことにする. (7/4/09 追記)
関数とは![]() の値に対して
の値に対して![]() の値がただ1つ定まる規則のことだが,
微分や積分など公式を使って式の計算をしていると,
「値」のことを忘れがちである.ある点の近くでの関数の値の大きさに注目し,
グラフや数値の計算を通してテイラーの定理の理解への第一歩となることを目指す.
の値がただ1つ定まる規則のことだが,
微分や積分など公式を使って式の計算をしていると,
「値」のことを忘れがちである.ある点の近くでの関数の値の大きさに注目し,
グラフや数値の計算を通してテイラーの定理の理解への第一歩となることを目指す.
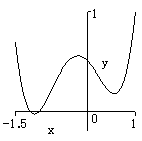 例1
例1
![]() の
の![]() の近くでの値を考えよう.
の近くでの値を考えよう.![]() のグラフは右の図のようになる.
のグラフは右の図のようになる.![]() の値が0に近いと
の値が0に近いと![]() より
より![]() は小さく,
は小さく,![]() ,
, ![]() は順に更に小さくなる.
したがって,
は順に更に小さくなる.
したがって,![]() を低い次数で打ち切った多項式の値は,
を低い次数で打ち切った多項式の値は,![]() の近くでは
の近くでは![]() の値に近いはずである.実際,
の値に近いはずである.実際,
![]() のグラフは下図の通りになる(
のグラフは下図の通りになる(![]() のグラフは点線で表示).
のグラフは点線で表示).
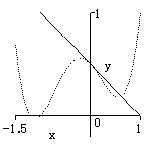
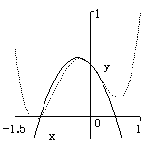
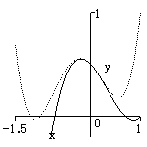
一番左の![]() は
は![]() における
における![]() の接線である.
の接線である.![]() の近くでは,
の近くでは,![]() と
と![]() の違いはグラフからは読み取りにくいが,
の違いはグラフからは読み取りにくいが,![]() に比べると
に比べると![]() に近づいているのがわかる.
たとえば,
に近づいているのがわかる.
たとえば,![]() における値を比べてみると,
における値を比べてみると,
![]()
のように次数を上げると値が近づいていくのがわかる.
![]() の
の![]() における接線の方程式は,
における接線の方程式は,![]() だから,
だから,![]() の係数,つまり
の係数,つまり![]() の定数項
の定数項![]() と1次の係
数
と1次の係
数![]() は
は
![]() により与えられていることがわかる.
2次以上の項の係数も微分と関係がある.
により与えられていることがわかる.
2次以上の項の係数も微分と関係がある.
一般の4次式![]() で考えよう.これに
で考えよう.これに![]() を代入すると,
を代入すると,![]() がわかり,
がわかり,![]() に
に![]() を代入すると
を代入すると![]() がわかる.さらに微分して
がわかる.さらに微分して![]() を代入することを続けていこう.
を代入することを続けていこう.![]() を
を![]() 回微分したものを
回微分したものを![]() と表す.
と表す.![]() に
に![]() を代入すると
を代入すると![]() ,2次の係数は
,2次の係数は![]() で与えられる.
で与えられる.![]() に
に![]() を代入すると
を代入すると![]() ,3次の係数は
,3次の係数は![]() で与えられる.
で与えられる.![]() だから,4次の係数は
だから,4次の係数は![]() で与えられる.こうして,4次多項式
で与えられる.こうして,4次多項式![]() は
は
![]()
のように係数を微分を用いて表すことができることがわかった.
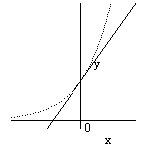 例2 多項式でない関数の例として指数関数
例2 多項式でない関数の例として指数関数![]() をとりあげよう.
をとりあげよう.![]() だから
だから![]() における
における![]() の接線の方程式は,
の接線の方程式は,![]() で与えられる.
で与えられる.![]() と
と![]() のグラフは右図のようになる.
のグラフは右図のようになる.![]() の近くで
の近くで![]() と
と![]() の値が近いことがグラフからわかる.
の値が近いことがグラフからわかる.
例1にならって,![]() から
から![]() 次多項式
次多項式
![]()
を作ろう.![]() より,
より,
![]()
となる.作り方から,
![]()
が成り立つ.
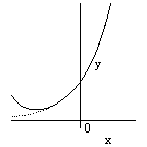
![]() のグラフは下図のようになる(
のグラフは下図のようになる(![]() のグラフは点線で表示).
のグラフは点線で表示).
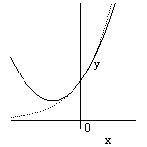
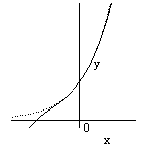
![]()
のように次数を上げると値が近づいていくのがわかる(小数点以下4桁の近似値).
![]() の近くで,
の近くで,![]() と
と![]() が「近い」ということを別の形で見てみよう.
が「近い」ということを別の形で見てみよう.![]() のとき,
のとき,
![]()
となる.
最後の等号は
![]() における
における
![]() の微分係数が
1
であることを表している.
の微分係数が
1
であることを表している.
![]() のとき,
のとき,
![]() であり,
であり,
![]() となる.
これは
となる.
これは![]() において
において![]() が連続であることを表している.
が連続であることを表している.![]() のとき,ロピタルの定理より,
のとき,ロピタルの定理より,
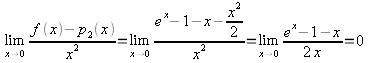
がわかる.一般の![]() の場合もロピタルの定理を繰り返し使うと,
の場合もロピタルの定理を繰り返し使うと,
![]()
であることがわかる.![]() の値がゼロに近いとき
の値がゼロに近いとき![]() は
は![]() が大きいほど小さいから,
上の式は
が大きいほど小さいから,
上の式は![]() がゼロに近づくとき
がゼロに近づくとき![]() は
は![]() よりもずっと速くゼロに近づくことを意味している.
よりもずっと速くゼロに近づくことを意味している.
指数関数を例に説明したが,一般の![]() の場合,
の場合,![]() の近くに限らず一般に
の近くに限らず一般に![]() の近くの場合
(テイラーの定理),
の近くの場合
(テイラーの定理),![]() (剰余項)の表示式(ラグランジュの剰余項)とその大きさの評価,などメインの話は教科書
(松木敏彦『理工系
微分積分』学術図書出版)に沿って授業で説明する.
(剰余項)の表示式(ラグランジュの剰余項)とその大きさの評価,などメインの話は教科書
(松木敏彦『理工系
微分積分』学術図書出版)に沿って授業で説明する.
(2009年5月2日作成)