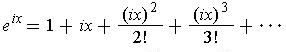
前回は， ベキ級数を用いた，オイラーの公式の「証明」を与えたが， 朝永氏も書いているように，形式的には見事だが，疑問の余地を残すものとなっている．少し長くなるが，ふたたび，朝永振一郎のエッセイ ｢数学がわかるというのはどういうことであるか｣から引用しよう．

ところが、やはり中学生より大きくなっていたので、 そのあと味悪さの原因がどこにあるかに気がついた。 どう気がついたかというと、この定理が出てくる前に、 数の虚数ベキの定義がやってないという点である。 ベキの定義はまず正の整数ベキから出発し、次に負数ベキが逆数と関係させて定義され、次に分数ベキが平方根とか立方根とかに関係させて定義されている。 ここまでは中学校で教えられた。さらに進んで無理数ベキは極限概念として微分学で習っている。ところが虚数ベキの定義になると、まだどこでも習ったことはない。 その習っていないものがいきなり式の左辺に出現したのだから理解できないのは当然である。 そういうことに気がついた。こう気がつくと、この定理の意味は一目りょう然となった。 つまり、これはむしろ虚数ベキの定義そのものなのであると、やはり高校生になると中学生のときとちがって、もやもやとわからないといっていないで、なぜわからないか、どこがわからない原因かと、つきとめることができたのであろうか。

1. ベキ級数 により， e ^ix を定義する．

2. オイラーの公式 により，e ^ix を定義する．

3. 別の方法で定義する．

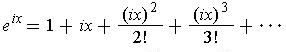
1 では，e ^x のテイラー展開において， x を ix で置き換えた級数を e ^ix の定義とするのである． 先に与えたオイラーの公式の証明ではこの点を明言していなかった． （無限和の収束，和の順序を交換して実数部分と虚数部分を集めてくる変形の正当化も必要であるが．）

2 では，cos x + i sin x を e ^ix と書いただけということになり，オイラーの「公式」は証明の対象ではなくなってしまう．ベキ級数を持ち出さなくて済むという意味では，もっとも簡易な定義である．

cos x と sin x のベキ級数展開と和の順序交換を既知として認めれば， 1 と 2 は同値である．これらが上の引用で朝永氏が「わかった」ことであろう． 3 については後述する予定であるが，さしあたり，1, 2 （のどちらか）を e ^ix の定義としたとして， 形式的な記号操作以上のものは何もないように見える． それだけのことであって， オイラーの公式に神秘的な意味を見出そうとするべきではないのだろうか？ 次回以降， e ^ix が e の虚数ベキ， あるいは「指数関数」 と呼ぶにふさわしい性質を持っているかどうかを問題にしよう． 1, 2 とは別の定義もこれに関連している． 次回は 2 の立場から次のことを考える．

実変数 x の複素数値関数 cos x + i sin x はどのような性質を持っているか？

(2001/05/14)

戻る