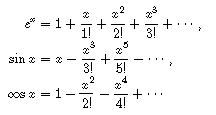
指数関数,正弦関数,余弦関数の x = 0 におけるテイラー展開
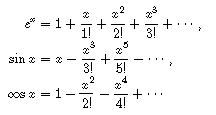
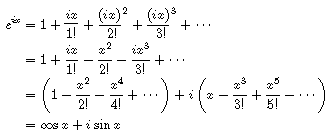
朝永振一郎 (1906〜1979, ノーベル物理学賞を受賞した日本を代表する物理学者)は,エッセイ 「数学がわかるというのはどういうことであるか」 (朝永振一郎 『科学者の自由な楽園』 江沢 洋(編集) 岩波文庫,2000 に所収) において,高校時代にオイラーの公式と出会ったときのことを次のように記している (今とは教育課程が違うので,学校の数学の授業で出てきたものと思われる).
幾何学的に定義された三角関数というものが、 指数関数という解析的なものと結びつくということは何とも脅威であったが、 それだけにまたその意味が理解できない、 証明はベキ級数を使ってやればいかにも簡単明りょう疑う余地はないが、 何かごまかされたみたいで、あと味が悪い、 ところが、やはり中学生より大きくなっていたので、 そのあと味悪さの原因がどこにあるかに気づいた。みなさんは,上の証明に納得しただろうか? また,納得できないとしたらその原因はどこにあるのだろうか?
(2001/04/03)