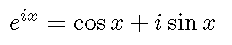
等式
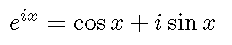
はオイラーによって1740年頃発見されたもので, オイラーの公式と呼ばれている.
左辺はネイピアの数 e を底とする指数関数,i は虚数単位 (i 2 = -1), 右辺の cos, sin はラジアンを単位とする正弦,余弦関数である.
この式の意味するところは,複素関数論を学べば完全に理解されるであろうが, 微分方程式,フーリェ級数論など実解析においても有用であり, また,この式自身が不思議な魅力をもっていることから,よく引き合いに出される.
吉田武 著の大ベストセラー『オイラーの贈物』(海鳴社, 1993), 『虚数の情緒』(東海大学出版会, 2000)において, オイラーの等式は「人類の至宝」, 「人類史に残る不朽の名作」と評され, その解説に多くのパルプが費やされている.
以下,オイラーの公式を巡って,私も何か書いてみようかと思うが, 更新は滞りがちになるだろうことを最初にお断りしておく.
(2001/04/03)