等式
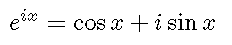
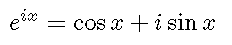
左辺はネイピアの数 e = 2.718... を底とする指数関数,i は虚数単位
(i 2 = -1),
右辺の cos, sin はラジアンを単位とする正弦,余弦関数です.
オイラーの公式は,
微分方程式,フーリェ級数論など実解析,
そして電気工学や物理学においても重要であり,
またこの式自身が不思議な魅力をもっていることから,よく引き合いに出されます.
オイラーの公式の「証明」を紹介するウエブページが多数存在することが,
関心の高さを感じさせます.
e ix = cos x + i sin x
を e ix の定義とする方法もあります
(オイラーの発見を尊重しない悪いやり方だという人もいますが,
数学ではよくやる手段です).
等式を証明するには,両辺に現れる式の意味がわかっている,
言い換えれば,両辺が数学的に定義されていることが前提となります.
右辺については,三角関数 cos x と sin x と複素数を既知とすれば,
cos x を実部,sin x を虚部とする複素数として定義されます.
左辺についてはどうでしょう.
実数 x を変数とする指数関数 ex
を既知としても,e の虚数乗 e i x
は何を意味するのでしょう?
たとえば,
(e i x)'= i e i x
が成り立つことを用いたオイラーの公式の「証明」は,
e i x を定義してから上の微分公式を証明しない限り,
正しいとは言えません.
(発見的な考察として,
あるい説明のための方便としての意義はあるかも知れませんが.
)
以下では,ベキ級数を用いた「証明」を紹介して,e i x
の定義について述べます.(関連する話題は,
2007年(オイラー生誕300年)に書いた解説 eπi +1 = 0 (pdfファイル,18ページ) にもあります.
また複素数の初歩的な解説からはじめて,
複素数平面の幾何学を用いた
オイラーの公式の証明を著書
『複素数とはなにか』(講談社ブルーバックス)に書きました.)
指数関数,正弦関数,余弦関数のベキ級数展開(マクローリン展開)
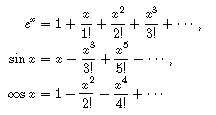
を既知とします.これは大学1年で学ぶ微分積分の重要事項です.
指数関数のベキ級数展開において,x を ix で置き換えて,
i 2 = -1 を用いて実数部分と虚数部分に分けると,
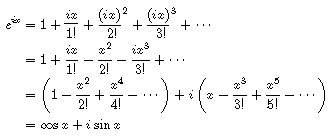
となり,
オイラーの公式 eix = cos x + i sin x
が証明されました.
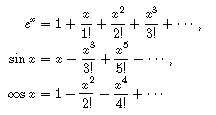
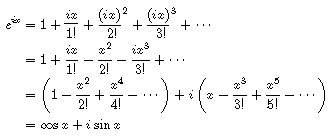
上の「証明」の問題点(e i x の定義はどこに隠れているか)
を指摘する朝永振一郎のエッセイを紹介します.
朝永振一郎 (1906〜1979,
ノーベル物理学賞を受賞した日本を代表する物理学者)は,エッセイ
「数学がわかるというのはどういうことであるか」
(朝永振一郎 『科学者の自由な楽園』 江沢 洋(編集) 岩波文庫,2000 に所収)
において,オイラーの公式と出会ったときのことを次のように記しています
(中学とあるのは旧制中学で卒業は17歳).
幾何学的に定義された三角関数というものが、 指数関数という解析的なものと結びつくということは何とも脅威であったが、 それだけにまたその意味が理解できない、 証明はベキ級数を使ってやればいかにも簡単明りょう疑う余地はないが、 何かごまかされたみたいで、あと味が悪い、 ところが、やはり中学生より大きくなっていたので、 そのあと味悪さの原因がどこにあるかに気づいた。 どう気がついたかというと、この定理が出てくる前に、 数の虚数ベキの定義がやってないという点である。 ベキの定義はまず正の整数ベキから出発し、次に負数ベキが逆数と関係させて定義され、次に分数ベキが平方根とか立方根とかに関係させて定義されている。 ここまでは中学校で教えられた。さらに進んで無理数ベキは極限概念として微分学で習っている。ところが虚数ベキの定義になると、まだどこでも習ったことはない。 その習っていないものがいきなり式の左辺に出現したのだから理解できないのは当然である。 そういうことに気がついた。こう気がつくと、この定理の意味は一目りょう然となった。 つまり、これはむしろ虚数ベキの定義そのものなのであると、やはり高校生になると中学生のときとちがって、もやもやとわからないといっていないで、なぜわからないか、どこがわからない原因かと、つきとめることができたのであろうか。
虚数ベキ e ix の定義こそが問題であると指摘されています. 上の「証明」は, 指数関数のベキ級数展開 e x において x を ix に置き換えた式を e ix の定義とすると, オイラーの公式が導かれるという証明になっています. (無限級数の収束、実部と虚部に分ける順序交換は絶対収束級数であることから正当な ものです.)あるいは, 上の「証明」(発見的議論)を念頭に置いて, オイラーの公式
オイラーの公式に関するより詳しい話は2007年(オイラー生誕300年)に書いた解説, 2012年刊行の著書もご覧下さい.
『複素数とはなにか』(講談社ブルーバックス)
(2009年4月23日作成, 2012年9月21日更新)