前回に引き続き微分積分の計算を Maple 12 でやってみた． （Maple で思うようにいかないところがあったので Maxima も使った．）演習問題を答えの検算も兼ねてやらせてみただけのことである． （注：微分積分Iの受講者の人はこの文章を読んでも勉強の足しにはならないでしょう． 授業では双曲線関数をやらずに指数関数の言葉でやっているので， cosh, sinh が出てきても反応できないでしょうが，それで構いません．）
曲線の長さの例としてよく出てくるカテナリーの長さを Maple で計算すると，

>    int(sqrt(1+(diff(cosh(x), x))^2), x = -1 .. 1);

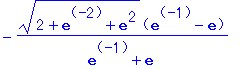
-(2+exp(-2)+exp(2))^(1/2)*(exp(-1)-exp(1))/(exp(-1)+exp(1))

のように根号を含む複雑な表示が得られた．この式を簡単にするために simplify, radnormal など思いつくコマンドを試してみたがうまくいかなかった． （Maple のコマンドを使って上の式を簡単にする方法がわかる方は教えて下さい． Maple13 ではどうなっている？）
上の式の根号の中身は (e+e-1)2 なので根号は外せるのだが， それを Maple にうまくやらせることができない． 根号の部分だけを取り出して Maple にやらせてみた． （Maple のコマンドを使って部分式を取り出す， 出力からコピー＆ペーストするという方法もあるが，ここでは改めて入力した．）

>    E := exp(1):

>    a := sqrt(E^2+2+E^(-2));

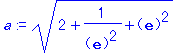
a := (2+1/(exp(1)^2)+exp(1)^2)^(1/2)

>    radnormal(%);

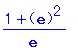
(1+exp(1)^2)/exp(1)

これなら簡単にしてくれた． （あっけなく簡単にしてくれたので，a とおいてそれを使っていない．） そもそも Maple が返した定積分の値は手計算ではまず辿らない道筋で得られているように見える． 不定積分を求めてみると次のようになり， やはり被積分関数の根号が外れて嬉しいというような人間的なことはやっていないようだ．

>    int(sqrt(1+(diff(cosh(x), x))^2), x);

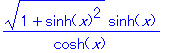
(1+sinh(x)^2)^(1/2)*sinh(x)/cosh(x)

そこで Student パッケージを用いて Maple に学習者向けのアドバイスを聞いてみることにする．

>    with(Student[Calculus1]):

>    Int(sqrt(1+(diff(cosh(x), x))^2), x=-1..1);

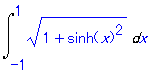
Int((1+sinh(x)^2)^(1/2),x = -1 .. 1)

>    Hint(%);

[rewrite, (1+sinh(x)^2)^(1/2) = cosh(x)]

>    Rule[%](%%);

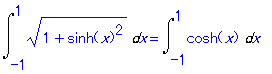
Int((1+sinh(x)^2)^(1/2),x = -1 .. 1) = Int(cosh(x),x = -1 .. 1)

すると根号を外すヒントを与えてくれる．答えを見ると次のようになる．

>    value(%);

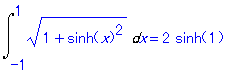
Int((1+sinh(x)^2)^(1/2),x = -1 .. 1) = 2*sinh(1)

最終的な答えとしては違和感を感じる．Maple は e を数学定数というより指数関数の1における値 exp(1) と見て， 特別扱いしていないからかも知れない． 指数関数に変換するとようやく微積分の教科書的な答えが得られる．

>    convert(rhs(%),exp);

exp(1)-exp(-1)

手計算と数式処理ソフトウエアでは計算の道筋が必ずしも同じではないし， 根号や三角関数（双曲線関数）を含む式の簡単化が難しいのは仕方がないのかと思いつつ， Maxima を起動した．Maxima は
integrate(sqrt(1+diff(cosh(x),x)^2),x,-1,1);
でいきなり %e-1(%e2-1) と教科書的な答えを出した． Maple が最初に出した根号を含む式も radcan を用いると簡単にしてくれた．
radcan(sqrt(%e^2+2+%e^(-2))*(%e-%e^(-1))/(%e+%e^(-1)));
今日のところは Maple より Maxima の方が人に優しいと感じた． これが無料で使えるとは何と素晴らしいことか．

(6/27/09)