Maple 12, Maxima, Sage に微分積分の授業で扱う例題や問題をやらせたり， Maple のヒント機能を用いて問題を作ったりした． これは解説ではなくそれに関連した覚書である． Maple 12 は商用，Maxima と Sage はフリーの数式処理ソフトウエアである．
Maple の Student パッケージには，積分計算のヒントを与えてくれる機能がある． まず Student[Calculus1] をロードする．

>    with(Student[Calculus1]):

置換積分の初歩的な例を考えてみよう．Maple では積分計算に int を用い， Int は未評価の積分を返す．ここでは積分計算のステップを知りたいので Int を用い， 積分を Int1 と名付けておく．

>    Int1 := Int(x*sqrt(x+1),x);

Int1 := Int(x*(x+1)^(1/2),x)

Hint 命令を実行すると，Maple は置換積分の置き方を教えてくれる．

>    Hint(Int1);

[change, x+1 = u^2, u]

Rule 命令により上のヒント（% で直前の結果を指す）を Int1 に適用した結果が得られる．

>    Rule[%](Int1);

Int(x*(x+1)^(1/2),x) = Int(-2*u^2+2*u^4,u)

この調子で1段階ずつ進んでいくことができるがあとは易しいので value 命令で積分の答えを出してしまおう． （結果だけに関心があるならこのような段階を踏まなくても int(x*sqrt(x+1),x) を実行すれば同じ結果が得られる．）

>    value(%);

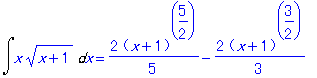
Int(x*(x+1)^(1/2),x) = 2/5*(x+1)^(5/2)-2/3*(x+1)^(3/2)

ここではコマンドラインの入力を示したが， IntTutor 命令を使うとボタンを配置した専用の入力画面が開いて，必要に応じて Maple からヒントをもらいながら自分で考えた変形を行い対話的に積分を計算することができる． （学生自身がこのような機能を使って勉強することの意義や効果はここでは検討しない．）

>    IntTutor();

有理関数の不定積分の例を挙げよう．

>    Int(1/(x^4+1),x);

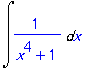
Int(1/(x^4+1),x)

この積分計算のヒントを尋ねると partialfractions（部分分数）と教えてくれる．

>    Hint(%);

[partialfractions]

このルール（直前の結果 %）を用いて積分（2つ前の結果 %%）を変形した結果を示す．

>    Rule[%](%%);

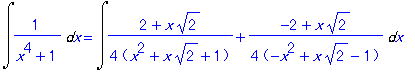
Int(1/(x^4+1),x) = Int(1/4*(2+x*2^(1/2))/(x^2+x*2^(1/2)+1)+1/4*(-2+x*2^(1/2))/(-x^2+x*2^(1/2)-1),x)

Maple は部分分数分解の形まで教えてくれた． 最後の答えまで見てしまおう．

>    value(%);

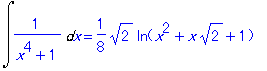
Int(1/(x^4+1),x) = 1/8*2^(1/2)*ln(x^2+x*2^(1/2)+1)+1/4*2^(1/2)*arctan(1/2*(2*x+2^(1/2))*2^(1/2))-1/8*2^(1/2)*ln(-x^2+x*2^(1/2)-1)-1/4*2^(1/2)*arctan(1/2*(-2*x+2^(1/2))*2^(1/2))
Int(1/(x^4+1),x) = 1/8*2^(1/2)*ln(x^2+x*2^(1/2)+1)+1/4*2^(1/2)*arctan(1/2*(2*x+2^(1/2))*2^(1/2))-1/8*2^(1/2)*ln(-x^2+x*2^(1/2)-1)-1/4*2^(1/2)*arctan(1/2*(-2*x+2^(1/2))*2^(1/2))
Int(1/(x^4+1),x) = 1/8*2^(1/2)*ln(x^2+x*2^(1/2)+1)+1/4*2^(1/2)*arctan(1/2*(2*x+2^(1/2))*2^(1/2))-1/8*2^(1/2)*ln(-x^2+x*2^(1/2)-1)-1/4*2^(1/2)*arctan(1/2*(-2*x+2^(1/2))*2^(1/2))

これは授業の教科書に使っている松木敏彦「理工系 微分積分」問12.3 (5) にある問題である． （x4 +1 の因数分解は高等学校で習わないものでやや高度な問題．）
Maple で部分分数に分解するには convert( , parfrac) を使うが，Maple は指定しないと分母を有理数係数の範囲でしか因数分解しないので， 今の例では望む結果が得られない．

>    convert(1/(x^4+1),parfrac,x);

1/(x^4+1)

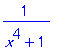
sqrt(2) を使えば分母が因数分解できることがわかっていれば，次のようにすることができる．

>    convert(1/(x^4+1),parfrac,x,sqrt(2));

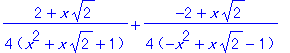
1/4*(2+x*2^(1/2))/(x^2+x*2^(1/2)+1)+1/4*(-2+x*2^(1/2))/(-x^2+x*2^(1/2)-1)

また次のように実数の範囲で数値的に部分分数分解を得ることもできる．

>    convert(1/(x^4+1),parfrac,x,real);

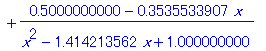
(.5000000000+.3535533907*x)/(x^2+1.414213562*x+1.000000000)+(.5000000000-.3535533907*x)/(x^2-1.414213562*x+1.000000000)
(.5000000000+.3535533907*x)/(x^2+1.414213562*x+1.000000000)+(.5000000000-.3535533907*x)/(x^2-1.414213562*x+1.000000000)

identify 命令を用いると，近似値から推測して厳密な式が復元される．

>    identify(%);

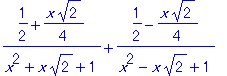
(1/2+1/4*x*2^(1/2))/(x^2+x*2^(1/2)+1)+(1/2-1/4*x*2^(1/2))/(x^2-x*2^(1/2)+1)

Maxima では integrate(1/(x^4+1),x) とすれば不定積分が計算できる． Maxima では部分分数分解は partfrac 命令により行うが，partfrac で sqrt(2) を含む形で拡大する方法は知らない． （factor(x^4+1,a^2-2）のように 2 の平方根 a を付加して分母の因数分解を行うことはできる．） また，有理数係数の多項式の範囲で分母が因数分解できる形 partfrac(1/(x^4+4*a^4),x) で実行すれば2次式を分母とする部分分数に分解することができる． これは Maple でも事情は同じである．
次の不定積分を考えよう．

>    Int(1/(x^2-1)^(1/2),x);

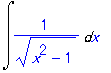
Int(1/((x^2-1)^(1/2)),x)

Maple は3通りの置換方法を教えてくれる．

>    Hint(%);

[change, x = sec(u), u], [change, 1-1/(x^2) = u^2, u], [change, u = (x^2-1)^(1/2)-x, u]

3番目が定石の置き方だが， 試しに2番目にしたがって変形すると有理式の積分になる （このまま進めて行くと，あるいは value 命令を使うと答えが得られるが， 教科書によく載っている表示まで Maple に変形させるのはかなり大変である． また，必ずしも実りある努力とは思えない．）

>    Rule[%[2]](%%);

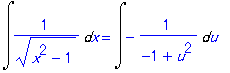
Int(1/((x^2-1)^(1/2)),x) = Int(-1/(-1+u^2),u)

次に松木敏彦「理工系 微分積分」例題12.10を Maple にやらせてみよう．

>    Int(1/(x^2*(1-x))^(1/3),x);

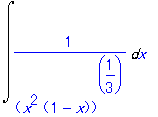
Int(1/((x^2*(1-x))^(1/3)),x)

>    Hint(%);

[]

ヒントが得られない．Maple に答えを出してもらうと， ガウスの超幾何関数を用いた結果が得られる．

>    value(%%);

3*x^(1/3)*hypergeom([1/3, 1/3],[4/3],x)

これは同書にある初等関数を使った答えと一致しているはずだが，少し試してみた範囲では Maple を用いて簡単化できなかった．Maxima は integrate(1/(x^2*(1-x))^(1/3),x) を実行すると，初等関数を使った答えを出力した． Maxima の出した答えは教科書にある答えとほぼ同じ形をしている． また，不定積分をさらに微分すると元の関数に戻るはずだが，Maxima が出した根号を含む分数式を簡単化して元の式に変形させることには成功していない． 差がゼロであることは ratsimp で確かめることができた． Sage はこの不定積分を求めることができなかった．
Maple が出した超幾何関数による不定積分の表示を微分して元に戻ることを Maple を使って確かめられるのかどうかわからない． 上の積分は同書の解説にあるように次のように変形できる．

>    Int((x/(1-x))^(1/3)/x,x);

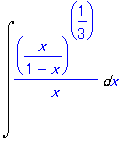
Int((x/(1-x))^(1/3)/x,x)

これについて Maple にヒントを聞いてみると，定石にある置換を教えてくれる．

>    Hint(%);

[change, x/(1-x) = u^3, u]

そしてそれにしたがって答えを出すこともできる．

>    Rule[%](%%);

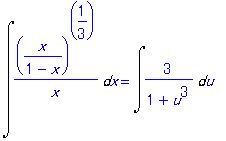
Int((x/(1-x))^(1/3)/x,x) = Int(3/(1+u^3),u)

>    value(%);

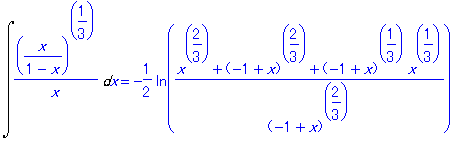
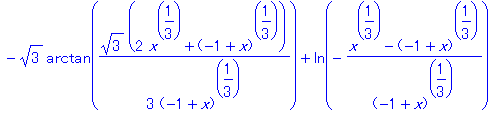
Int((x/(1-x))^(1/3)/x,x) = -1/2*ln((x^(2/3)+(-1+x)^(2/3)+(-1+x)^(1/3)*x^(1/3))/(-1+x)^(2/3))-3^(1/2)*arctan(1/3*3^(1/2)*(2*x^(1/3)+(-1+x)^(1/3))/(-1+x)^(1/3))+ln(-(x^(1/3)-(-1+x)^(1/3))/(-1+x)^(1/3))
Int((x/(1-x))^(1/3)/x,x) = -1/2*ln((x^(2/3)+(-1+x)^(2/3)+(-1+x)^(1/3)*x^(1/3))/(-1+x)^(2/3))-3^(1/2)*arctan(1/3*3^(1/2)*(2*x^(1/3)+(-1+x)^(1/3))/(-1+x)^(1/3))+ln(-(x^(1/3)-(-1+x)^(1/3))/(-1+x)^(1/3))

ところが int 命令を使って int((x/(1-x))^(1/3)/x,x) とすると Maple はやり方を知っているはずの答えを出してくれない． Maxima は integrate((-x/(-1+x))^(1/3)/x,x) で答えを出してくれた． Sage も Maxima と同じ入力で答えを出してくれた． 手計算や数式処理ソフトウエアを用いて計算できる範囲でも色々悩ましいことが起こるものだ． ここでは教科書にある積分を数式処理ソフトウエアにやらせてみる以上の明確な目的意識に乏しいので， 得られた結果に満足するかどうかも判然としない． 数式処理ソフトウエアに何をやらせるか， 得られた結果をどう理解して先に進んでいくかを適切に判断するには， 天下り的な課題であれ何らかの目標設定，数式処理ソフトウエア独特の操作への慣れ， 数学的能力が必要だろう． 私のクラスの1年生は来年度に授業で数式処理ソフトウエアに出会うが， 効果的な学びに結び付けていけるのか未知の部分が大きい． ちなみに，初等関数で答えが表せる不定積分の計算は Axiom が優れているそうだ． 日本語版がもうじきリリースされる Maple 13 では変化があるだろうか．
話が脱線してしまった． 数式処理ソフトウエアが答えを出してくれても実際内部でどのような処理を行っているかユーザにはわからない． （Maple では infolevel を上げて処理のステップを多少見ることはできるが限定的である． Maxima などのオープンソースの数学ソフトウエアや（多くの）プログラムソースを表示できる Maple では，ユーザーが内部の処理を知ることが原理的には可能であるが実際は大変だろう．） また数式処理ソフトウエアがやっている積分計算のアルゴリズムと標準的に教えられる積分計算法が完全に一致しているわけではない． とはいえ，Maple のヒント機能は標準的な教程の範囲で答えに至るステップを示してくれる点で， 教員の教材開発に役に立つものと思う（と無理やりまとめておく）．

(6/6/09)