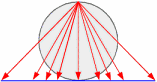
球面上に光源を置いて,
中心をはさんで反対側の点で接する平面にうつった像を対応させる.
これにより,光源を置いた点を除く球面上の点は,平面上の点と1対1に対応する
(右図参照).
この対応を立体射影といいます.立体射影は角度を保つことが知られている.
冒頭のアニメーションは,
地球の自転を赤道上に視点を置いて平面上に立体射影したものである.
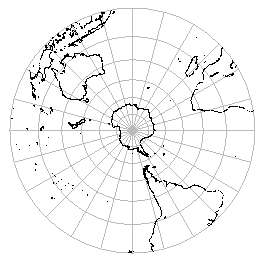
北極に視点を置いて,
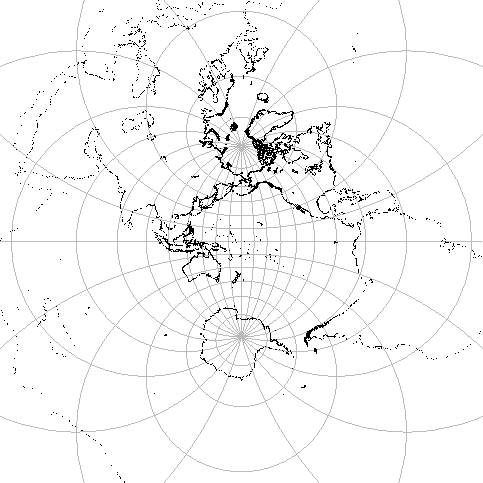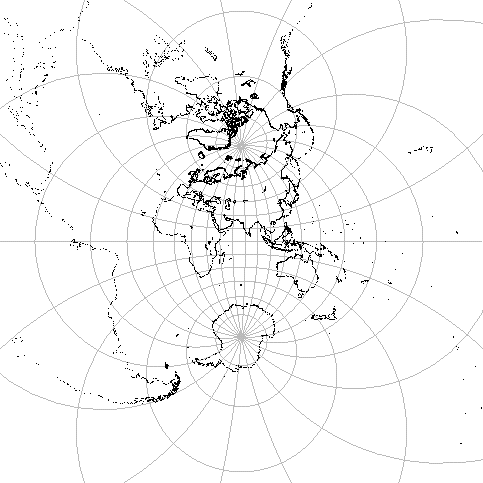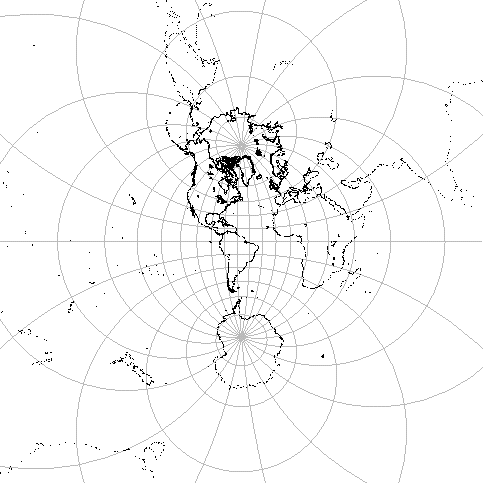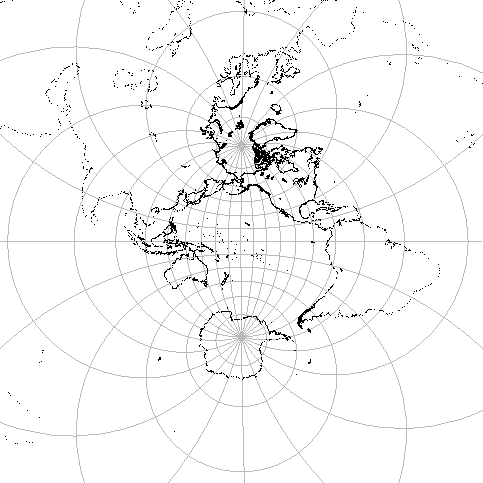
南極における接平面上に立体射影すると南半球は図1のようになる.
これは地球を裏側から見ていることになるので,左右を反転すると,
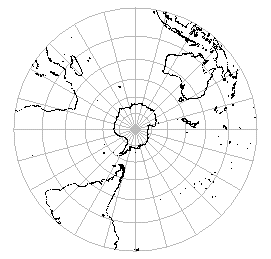
表側から見た図になる(図2).上のアニメーションや以下の例では,
同様に地表から見た図を示している.
|
|
| 図1 | 図2 |
立体射影は,北極を除いた球面から平面の上への1対1写像である.
範囲を広げて北半球(の1部)も表示すると図3のようになる.
立体射影は,等角写像であることに特徴がある(裏側から見た場合,
角の向きは逆になる).
図の中心は南極だが,半径が大きくなると北極に近づいていく.

図3
視点を変えると,東半球の地図が得られる(図4).
(北極を視点として立体射影すると,東半球は上半平面内に対応している.)
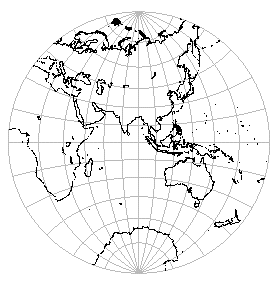
赤道上の経度180°の点から立体射影すると,
経度0緯度0の点を中心とする地図が得られる(図5).
赤道上に視点を置いて地球を自転させたのが冒頭のアニメーションである.
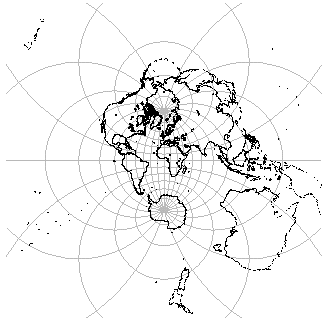
図5
これらの図は,数学ソフトウエア Maple と V. Costanzo 氏による
The Maple Maptools Package を用いて作成した.
岡山理科大学における大学院の講義の準備で,
リーマン球面から複素平面への立体射影,
そして回転群と特殊ユニタリ群の関係について計算ていたら,
立体射影により世界地図を描いたり,
地球の自転をアニメーションにしたくなったのである.
このパッケージでは,
地球上の点に対応させる平面上の点を緯度と経度の数式により指定して,
地図を描くことができる.
立体射影以外のいろいろな地図投影法を試してみるのもおもしろいだろう.
立体射影についてもっと知りたい人は,複素関数論の教科書を参照して下さい.
(2005年5月15日作成(2009年4月24日修正して再公開))