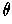 に取り換えて,関数
に取り換えて,関数
更新を思い切りさぼってしまったが,前回の続き.
オイラーの公式の右辺に現れる複素数値関数 cos x + i sin x がどういう性質を持っているか? を問題にする.
後で幾何的に考える都合上,変数を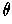 に取り換えて,関数
に取り換えて,関数
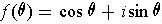
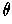 は実変数, i は虚数単位である.
積
は実変数, i は虚数単位である.
積
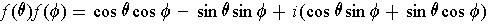
を作ってみると,これは三角関数の加法定理により,
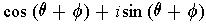 に等しい.つまり次の式が成り立つことがわかる.
に等しい.つまり次の式が成り立つことがわかる.
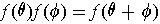
今,
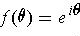 と「書き表す」ことにすると,上の式は次のようになる.
と「書き表す」ことにすると,上の式は次のようになる.
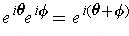
e の肩に乗っているのが虚数である点を除けば, この式は「指数法則」の形をしている. 指数法則は指数関数の重要な性質であるから, f は指数関数によく似ているということができるだろう.
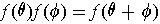
において変数の値が等しいとすると,特に
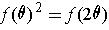
が得られる.数学的帰納法により,自然数 n に対して,
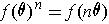
が成り立つことが証明できる(やってみて下さい). これを f の定義に戻って書き下すと次のようになる.
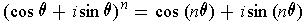
この式は,ドモアブルの公式と呼ばれる. 左辺を展開して実部や虚部をとると,cos, sin の n 倍角の公式を導くことができる(試しに3倍角の公式を導いてみては?). ドモアブルの公式は,先の指数関数を模した記号を使えば, 次のように書くこともできる.
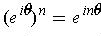
複素数の実部を x,虚部を y として, 複素数を xy 直交座標系上の点として表すことができる. このように見た座標平面を,複素平面(現行の数学Bの教科書では, 複素数平面)という. 考えた人の名前をとって,アルガン図,あるいはガウス平面とも呼ばれる. f が満たす「指数法則」 やドモアブルの公式は複素平面の幾何から見ると何を表しているだろうか? (図を描くのが面倒なので)これは次回に回すことにする.
上では,三角関数の加法定理から
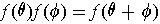
が導かれると言ったが,逆にこの式の実部と虚部をとれば, cos と sin の加法定理が導かれる(ピンと来なければ確かめてみよ). つまり, 三角関数の加法定理と f が満たす「指数法則」は同値なのである.
次回(と次々回)の予定:複素平面の幾何から見た f の「指数法則」および三角関数の加法定理を論じる. (2001/08/28)