数学ソフトウェア Maple の紹介

示野信一
http://sci-tech.ksc.kwansei.ac.jp/~shimeno/
shimeno "at" kwansei.ac.jp
2010年4月12日（旧版 2003年8月7）
関西学院大学理工学部数理科学科 

 

Maple や Mathematica, Maxima などのコンピュータソフトウェアは数学の計算や探求を行うための革新的なソフトウェアです。これらのソフトウェアは、 

 

 1 数値の計算 

 2 数式の計算 

 3 グラフィックス 

 

を統合的に扱うことができる点に特徴があります。数式の計算が行える部分を強調した、「数式処理ソフトウェア」または「計算機代数システム」という呼び方をされることもあります。統合的なプログラミング環境も提供されています。様々な数学の関数やコマンドが用意されているので、BASIC, C などの伝統的なプログラミング言語に比べて容易に望む結果を得ることができます。 

 

関西学院大学では Maple のキャンパスライセンスを有しているので、キャンパス内のコンピュータで自由に Maple を使うことができます。また、所属学生は自宅のパソコンに Maple をインストールして使用することもできます。 

 

Maple とは？

Maple （メイプル）は1980年代にカナダの Waterloo 大学で開発され、現在はWaterloo Maple 社が 開発・販売している数学ソフトウェアです。パソコンやワークステーション上で使用することができます。現在の最新バージョンは Maple 13 です。数理演習室や学内のコンピューター実習室には Maple がインストールされています。 

 

Maple はメニューやマニュアル、オンラインで参照できるヘルプの日本語化が進められています。開発元のホームページでは、科学技術分野、教育分野など幅広い分野における Maple の使用例が公開されており、日本の代理店のサイバネットシステムのホームページでも日本語で参照できる利用例が公開されています。 

 

Maple の特徴 

 

　数式の計算 （整式、方程式、微分積分） 

　数値の計算 （任意精度） 

　グラフィックス （平面、空間、アニメーション） 

　プログラム言語 

　ワークシートインタフェースで対話的に利用できる （マウスとキーボード） 

　多くの拡張パッケージ （線形代数、数学学習、統計、整数論、科学単位など） 

　ワークシート、グラフィックスの外部出力 

　ウェブで多くの情報が提供されている 

　関西学院大学では Maple のキャンパスライセンスを有しているので、キャンパス内のコンピュータで自由に Maple を使うことができる 

 

数の計算 

簡単な計算 

百聞は一見にしかず、実際に Maple を使ってみましょう。 

 

1. Maple のアイコンをダブルクリックする (Maple の起動） 

2. プロンプト > からコマンドを入力する 

3. エンターキーを押す (コマンドの実行） 

 

簡単な計算を実行してみましょう。 

> `+`(1, 1)
 

2 (2.1.1)
 

割り算は / により入力します。 

> `+`(`/`(1, 3), `/`(1, 2))
 

`/`(5, 6) (2.1.2)
 

Maple は自動的に通分した結果を返します。 

 

掛け算は * により入力します。 

> `*`(13, 17)
 

221 (2.1.3)
 

ベキ乗には ^ を使います。 

> `^`(2, 100)
 

1267650600228229401496703205376 (2.1.4)
 

厳密な数と近似値 

evalf( ) コマンドにより近似値を計算することができます。 

> evalf(`/`(1, 3))
 

.3333333333 (2.2.1)
 

数に小数点が含まれていると自動的に近似値が得られます。 

> `+`(2.0, `/`(1, 7))
 

2.142857143 (2.2.2)
 

次の結果と比較してみて下さい。 

> `+`(2, `/`(1, 7))
 

`/`(15, 7) (2.2.3)
 

平方根は sqrt( ) 関数により与えられます。 

> sqrt(26)
 

`*`(`^`(26, `/`(1, 2))) (2.2.4)
 

> evalf(sqrt(26))
 

5.099019514 (2.2.5)
 

evalf( ) コマンドに桁数を与えることにより、標準の値 10 桁から変更することができます。 

> evalf(sqrt(26), 20)
 

5.0990195135927848300 (2.2.6)
 

円周率 

> Pi
 

Pi (2.2.7)
 

> evalf(Pi, 100)
 

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068		 (2.2.8)
 

数式の計算

Maple は式の計算や微分積分など様々な計算ができます。 

 

文字式の展開には expand( ) 、因数分解には factor( ) を使います。 

`*`(`^`(`+`(a, b), 2)) の展開 

> expand(`*`(`^`(`+`(a, b), 2)))
 

`+`(`*`(`^`(a, 2)), `*`(2, `*`(a, `*`(b))), `*`(`^`(b, 2))) (3.1)
 

`*`(`^`(`+`(a, b), 3)) の展開 

> expand(`*`(`^`(`+`(a, b), 3)))
 

`+`(`*`(`^`(a, 3)), `*`(3, `*`(`^`(a, 2), `*`(b))), `*`(3, `*`(a, `*`(`^`(b, 2)))), `*`(`^`(b, 3))) (3.2)
 

`+`(`*`(`^`(x, 6)), `-`(1)) の因数分解 

> factor(`+`(`*`(`^`(x, 6)), `-`(1)))
 

`*`(`+`(x, `-`(1)), `*`(`+`(x, 1), `*`(`+`(`*`(`^`(x, 2)), x, 1), `*`(`+`(`*`(`^`(x, 2)), `-`(x), 1))))) (3.3)
 

`+`(`*`(`^`(x, 4)), 64) の因数分解 

> factor(`+`(`*`(`^`(x, 4)), 64))
 

`*`(`+`(`*`(`^`(x, 2)), `-`(`*`(4, `*`(x))), 8), `*`(`+`(`*`(`^`(x, 2)), `*`(4, `*`(x)), 8))) (3.4)
 

結果はちょっと意外だったかもしれません。 

 

分数式の計算をすることもできます。 

> `+`(`/`(1, `*`(x)), `-`(`/`(1, `*`(`+`(x, 1)))))
 

`+`(`/`(1, `*`(x)), `-`(`/`(1, `*`(`+`(x, 1))))) (3.5)
 

式を通分するには normal( ) を使います。直前の結果は入力し直さなくても % により参照することができます。 

> normal(%)
 

`/`(1, `*`(x, `*`(`+`(x, 1)))) (3.6)
 

分数式  `+`(`/`(1, `*`(`+`(a, `-`(b)), `*`(`+`(a, `-`(c))))), `/`(1, `*`(`+`(b, `-`(c)), `*`(`+`(b, `-`(a))))), `/`(1, `*`(`+`(c, `-`(a)), `*`(`+`(c, `-`(b))))))  を通分してみましょう。 

> `+`(`/`(1, `*`(`+`(a, `-`(b)), `*`(`+`(a, `-`(c))))), `/`(1, `*`(`+`(b, `-`(c)), `*`(`+`(b, `-`(a))))), `/`(1, `*`(`+`(c, `-`(a)), `*`(`+`(c, `-`(b))))))
 

`+`(`/`(1, `*`(`+`(a, `-`(b)), `*`(`+`(a, `-`(c))))), `/`(1, `*`(`+`(b, `-`(c)), `*`(`+`(b, `-`(a))))), `/`(1, `*`(`+`(c, `-`(a)), `*`(`+`(c, `-`(b)))))) (3.7)
 

> normal(%)
 

0 (3.8)
 

`+`(`/`(`*`(`^`(a, 2)), `*`(`+`(a, `-`(b)), `*`(`+`(a, `-`(c))))), `/`(`*`(`^`(b, 2)), `*`(`+`(b, `-`(c)), `*`(`+`(b, `-`(a))))), `/`(`*`(`^`(c, 2)), `*`(`+`(c, `-`(a)), `*`(`+`(c, `-`(b))))))  ではどうでしょうか。分子の2乗を3乗にするとどうでしょう。 

 

関数のグラフ

関数のグラフを描くには plot コマンドを使います。 

 

y = `*`(`^`(x, 2)) の x = -1 から 1 までのグラフを描きます。範囲の指定の仕方に注意しましょう。 

> plot(`*`(`^`(x, 2)), x = -1 .. 1)
 

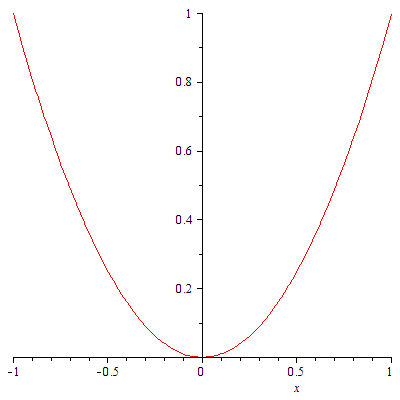Plot_2d
 

y = sin(x)　の　`+`(`-`(Pi))　から　Pi までのグラフを描きます。関数の変数は ( ) で囲んでいること、Pi　は Pi と入力していることに注意して下さい。三角関数の変数の単位は数学Cや数学IIIで学ぶ弧度法（ラジアン）を使っています。 

> plot(sin(x), x = `+`(`-`(Pi)) .. Pi)
 

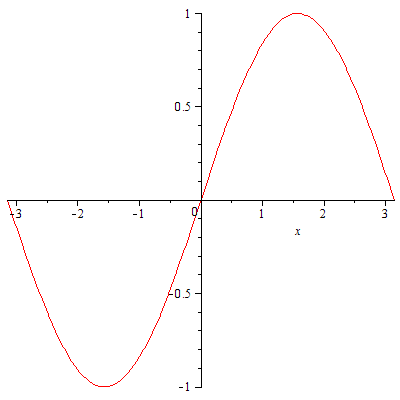Plot_2d
 

x 軸と y 軸の縦横比が 1:1 でないのが気になるようなら、グラフをクリックすると現れるメニューバー上の 1:1 ボタンを押すか、次のように scaling=constrained を付け加えます。 

> plot(sin(x), x = `+`(`-`(Pi)) .. Pi, scaling = constrained)
 

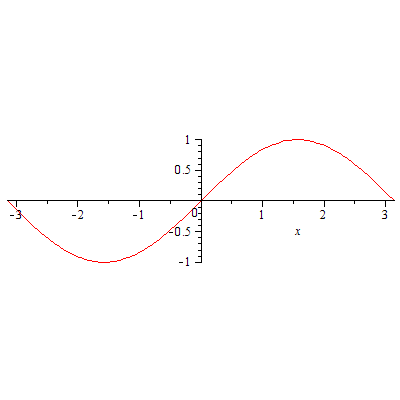Plot_2d
 

式の形をいろいろと変えてグラフを描いてその結果を考察してみるとおもしろいでしょう。 

> plot(sin(`+`(`*`(2, `*`(x)))), x = `+`(`-`(Pi)) .. Pi, scaling = constrained)
 

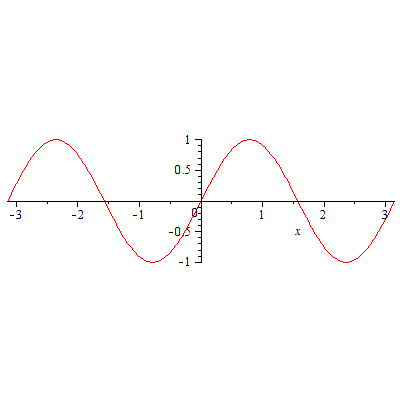Plot_2d
 

> plot(`+`(`*`(2, `*`(sin(x)))), x = `+`(`-`(Pi)) .. Pi, scaling = constrained)
 

Plot_2d
 

> plot(`+`(sin(x), cos(x)), x = `+`(`-`(Pi)) .. Pi, scaling = constrained)
 

Plot_2d
 

> plot(`*`(`^`(sin(x), 2)), x = `+`(`-`(Pi)) .. Pi, scaling = constrained)
 

Plot_2d
 

{ } で囲んで与えることにより、複数のグラフを一緒に描くこともできます。 

> plot({`+`(`*`(2, `*`(x)), 1), `+`(`*`(`^`(x, 2)), `*`(2, `*`(x)), 1)}, x = -4 .. 4)
 

Plot_2d
 

高等学校の範囲外ですが、plot3d コマンドを使うと、3次元空間の曲面を描くこともできます。x と y の式、x の範囲、y の範囲を plot3d コマンドに与えます。axes=boxed により箱型の座標軸を付け加えます（axes=normal とすると通常の座標軸が表示されます）。 

> plot3d(`+`(`*`(`^`(x, 2)), `-`(`*`(`^`(y, 2)))), x = -2 .. 2, y = -2 .. 2, axes = boxed); 1
 

Plot
 

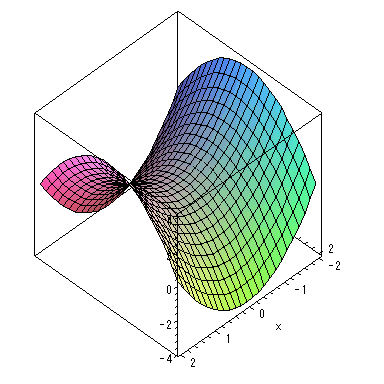マウスで図をクリックしたままドラッグすると、曲面を動かしていろいろな方向から見ることができます。 

> plot3d(`*`(sin(x), `*`(sin(y))), x = `+`(`-`(`*`(2, `*`(Pi)))) .. `+`(`*`(2, `*`(Pi))), y = `+`(`-`(`*`(2, `*`(Pi)))) .. `+`(`*`(2, `*`(Pi)))); 1
 

Plot
 

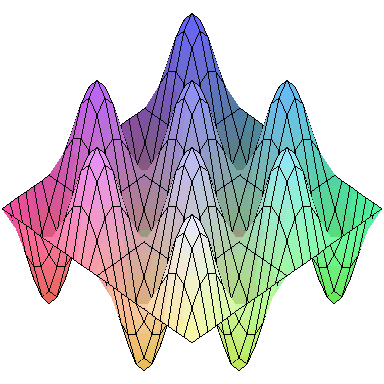f を定義して3次元プロット，等高線図，密度プロットを描いてみます。 

> `:=`(f, `*`(`+`(`*`(`^`(x, 2)), `+`(`*`(2, `*`(`^`(x, 2))))), `*`(exp(`+`(`-`(`*`(`^`(x, 2))), `-`(`*`(2, `*`(`^`(y, 2)))))))))
 

`+`(`*`(3, `*`(`^`(x, 2), `*`(exp(`+`(`-`(`*`(`^`(x, 2))), `-`(`*`(2, `*`(`^`(y, 2)))))))))) (4.1)
 

> plot3d(f, x = -2 .. 2, y = -1.5 .. 1.5)
 

Plot
 

> with(plots); -1
 

> contourplot(f, x = -2 .. 2, y = -1.5 .. 1.5)
 

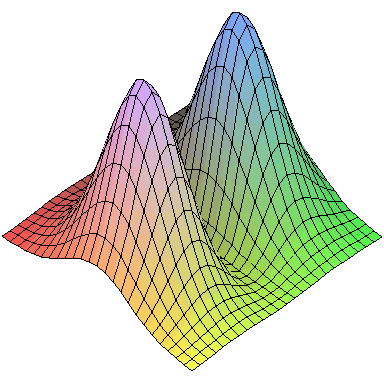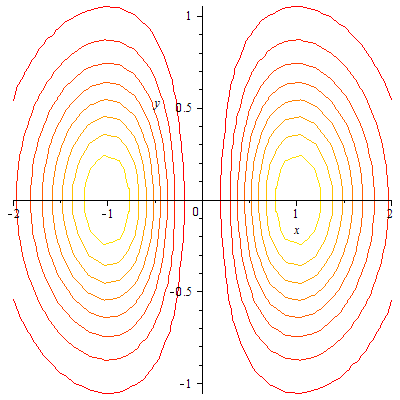Plot_2d
 

> densityplot(f, x = -2 .. 2, y = -1.5 .. 1.5, style = patchnogrid, axes = none)
 

Plot_2d
 

いろいろな曲線

数学Cで学ぶいろいろな曲線を Maple を使って描いてみましょう。 

 

最初に次のように入力しておきます。 

> with(plots); -1
 

> setoptions(scaling = constrained)
 

 

<媒介変数で表された曲線 

媒介変数で表された曲線を描くには、x 座標、y 座標、媒介変数の範囲を [ ] で囲んで、plot コマンドに与えます。 

 

例1 x = cos(t) ,  y = sin(t) 

> plot([cos(t), sin(t), t = 0 .. `+`(`*`(2, `*`(Pi)))])
 

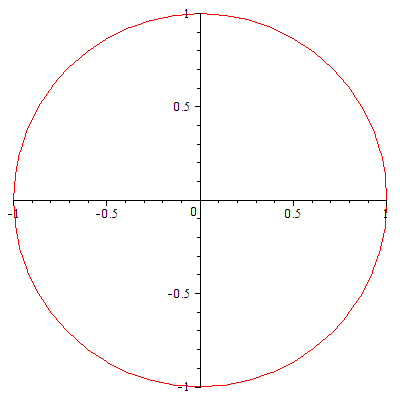Plot_2d
 

例2 x = cos(`+`(`*`(7, `*`(t))))  ,  y = sin(`+`(`*`(3, `*`(t)))) 

> plot([cos(`+`(`*`(7, `*`(t)))), sin(`+`(`*`(3, `*`(t)))), t = 0 .. `+`(`*`(2, `*`(Pi)))])
 

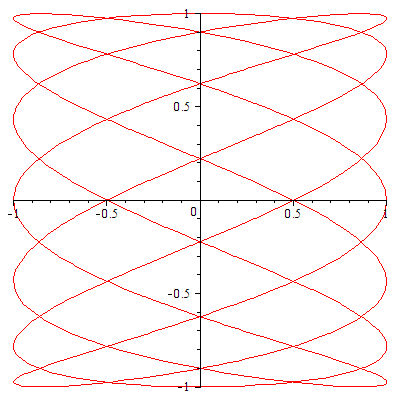Plot_2d
 

cos の中の 7 や sin の中の 3 を別の値に変えてみるとどうなるでしょう。 

 

例3 x = sin(`+`(`*`(2, `*`(t)))),  y = sin(`+`(`*`(3, `*`(t)))) 

> plot([sin(`+`(`*`(2, `*`(t)))), sin(`+`(`*`(3, `*`(t)))), t = 0 .. `+`(`*`(2, `*`(Pi)))]); 1
 

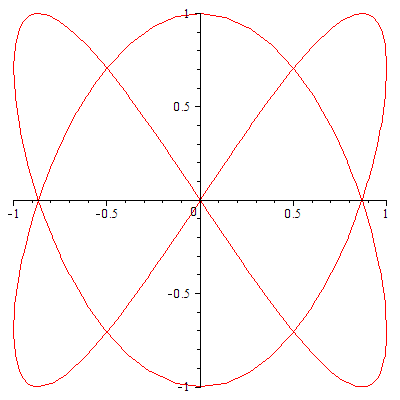Plot_2d
 

例4 x = `+`(cos(t), `*`(5, `*`(cos(`+`(`*`(3, `*`(t))))))),  y = `+`(`*`(6, `*`(cos(t))), `-`(`*`(5, `*`(sin(`+`(`*`(3, `*`(t)))))))) 

> plot([`+`(cos(t), `*`(5, `*`(cos(`+`(`*`(3, `*`(t))))))), `+`(`*`(6, `*`(cos(t))), `-`(`*`(5, `*`(sin(`+`(`*`(3, `*`(t)))))))), t = 0 .. `+`(`*`(2, `*`(Pi)))]); 1
 

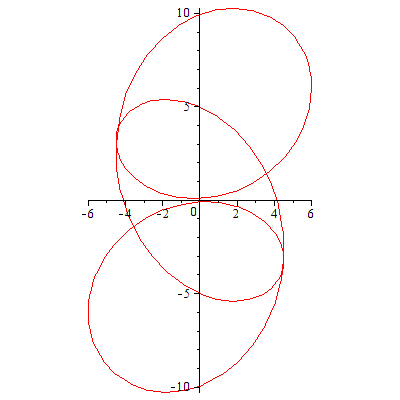Plot_2d
 

極方程式で与えられた曲線 

（まだ実行していなければ with(plots): setoptions(scaling=constrained) を1度実行しておいて下さい。） 

極方程式で与えられた曲線を描くには polarplot コマンドを使います。 

 

以下続けて座標軸を表示させないようにするために次の設定をしておきます。 

 

> setoptions(axes = none)
 

 

例1 r = 1 

> polarplot(1)
 

Plot_2d
 

例2 r = sin(`+`(`*`(4, `*`(theta)))) 

> polarplot(sin(`+`(`*`(4, `*`(theta)))))
 

Plot_2d
 

theta （シータ） と打ち込むのは面倒なら、偏角に別の記号を使っても構いません。以下では t を使います。 

 

例3 r = t 

> polarplot(cos(t))
 

Plot_2d
 

偏角の範囲を指定することもできます。 

例4 r = t  (t = 0 .. `+`(`*`(4, `*`(Pi)))) 

> polarplot(t, t = 0 .. `+`(`*`(4, `*`(Pi))))
 

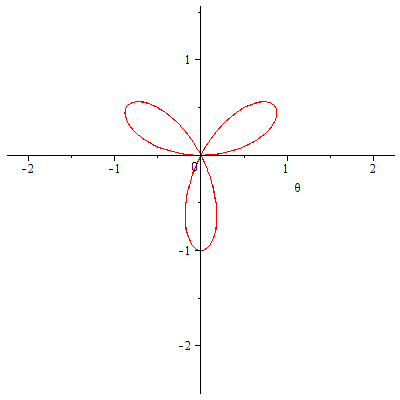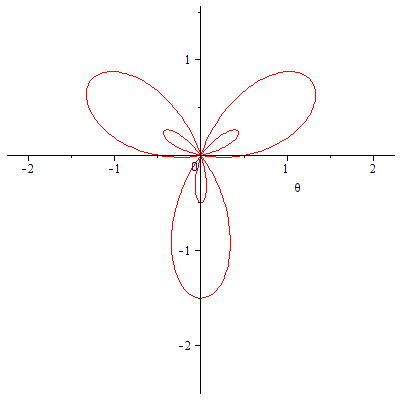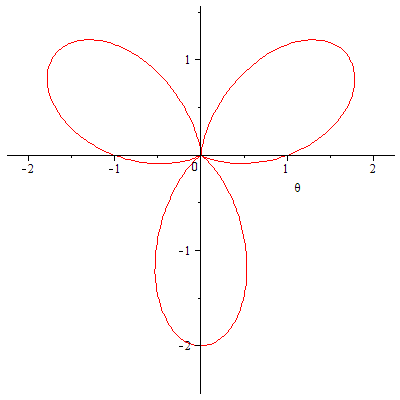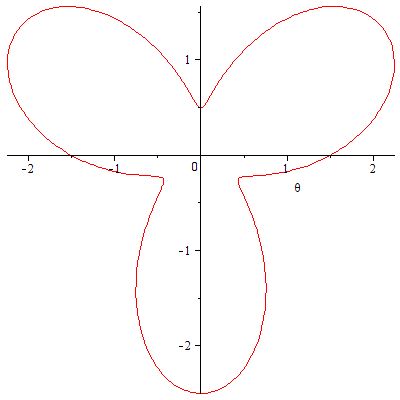
Plot_2d
 

 

問題　次の極方程式で与えられる曲線を描いてみてください。 

 

r = `+`(2, sin(`+`(`*`(8, `*`(t)))), `/`(`*`(sin(`+`(`*`(64, `*`(t))))), `*`(t))) 

 

r = `+`(exp(sin(t)), `-`(`*`(2, `*`(cos(`+`(`*`(4, `*`(t))))))), `*`(`^`(sin(`+`(`*`(`/`(1, 12), `*`(t)))), 15)))  (t = 0 .. `+`(`*`(24, `*`(Pi)))) 

 

Maple では、exp(sin(t)) は exp(sin(t)) と入力します。  

 

 

アニメーション

Maple を使ってアニメーションを作るのはとても楽しいものです。 

アニメーションの原理はテレビや映画と同じ原理で、連続した絵が次々とすばやく表示されると絵が動いて見えるという訳です。 

 

plots パッケージのコマンド animate によってアニメーションを作ります。たとえば、次の例は y = sin(`*`(a, `*`(x))) のグラフで a を 1 から 2 まで少しずつ変化させた一連のグラフィックスを表示します。 （一旦 restart してメモリー上の情報を消去します。） 

 

> restart
 

> with(plots); -1
 

> animate(sin(`*`(a, `*`(x))), x = 0 .. `+`(`*`(2, `*`(Pi))), a = 1 .. 2)
 

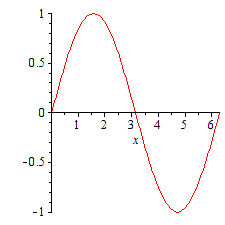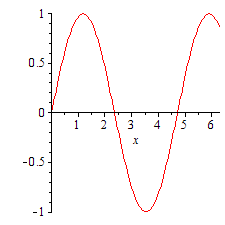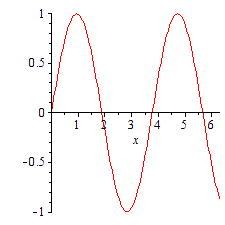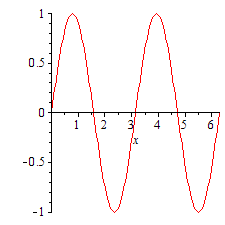Plot_2d
 

アニメーションを再生するには、まず得られた図をクリックして選択し、上方に現れたメニュー上の再生ボタンを押します。 

 

次の3つの例では、パラメータ a を変化させて放物線を動かしています。 

> animate(`*`(a, `*`(`^`(x, 2))), x = -3 .. 3, a = -4 .. 4)
 

Plot_2d
 

> animate(`+`(`*`(`^`(x, 2)), a), x = -3 .. 3, a = -4 .. 4)
 

Plot_2d
 

> animate(`*`(`^`(`+`(x, `-`(a)), 2)), x = -12 .. 12, a = -4 .. 4); 1
 

Plot_2d
 

 

極方程式で与えられた曲線のアニメーションの例。オプション coords=polar により極方程式であることを指定しています。 

numpoints を増やすと計算する点の数が増えて曲線が滑らかになります。 

> plot(sin(`+`(`*`(3, `*`(theta)))), theta = 0 .. `+`(`*`(2, `*`(Pi))), coords = polar)
 

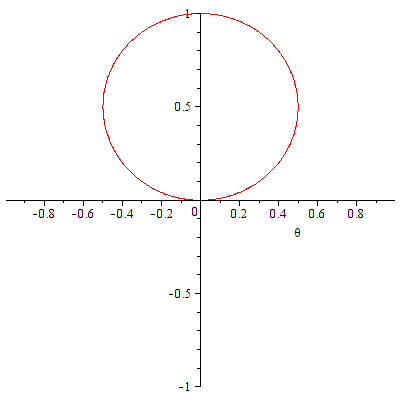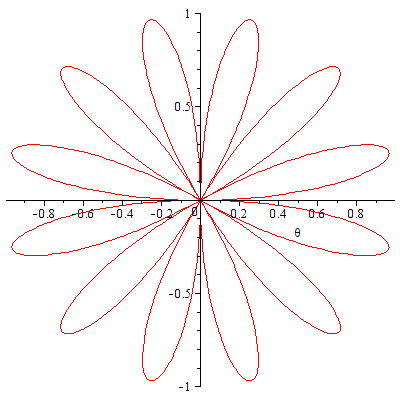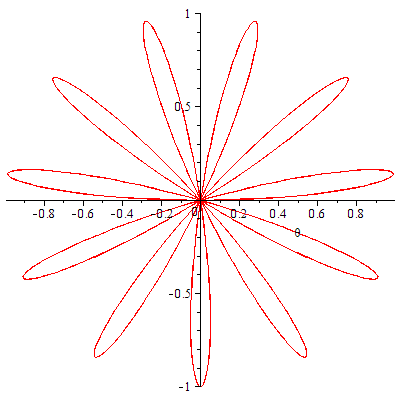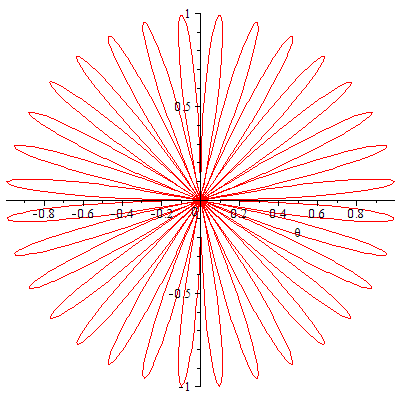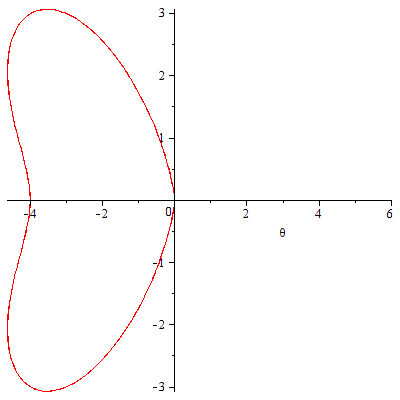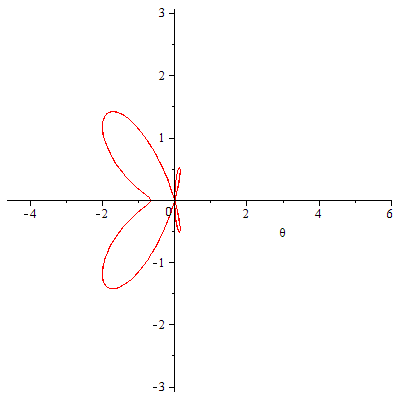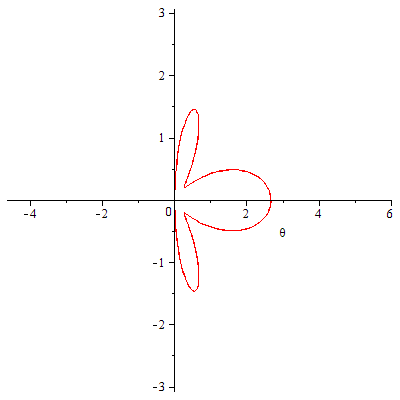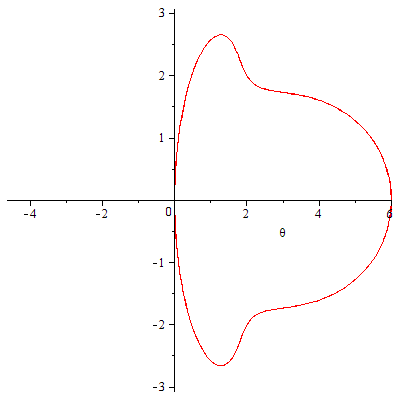Plot_2d
 

> animate(sin(`*`(a, `*`(theta))), theta = 0 .. `+`(`*`(2, `*`(Pi))), a = 1 .. 16, coords = polar, numpoints = 500)
 

Plot_2d
 

> animate(`+`(a, sin(`+`(`*`(3, `*`(theta))))), theta = 0 .. `+`(`*`(2, `*`(Pi))), a = 0 .. 1.5, coords = polar, numpoints = 200)
 

Plot_2d
 

> animate(`+`(cos(`+`(`*`(5, `*`(theta)))), `*`(a, `*`(cos(theta)))), theta = 0 .. `+`(`*`(2, `*`(Pi))), a = -5 .. 5, coords = polar, numpoints = 200); 1
 

Plot_2d
 

問題  思い思いの式を入力してアニメーションを作ってみて下さい。期待通りのアニメーションが得られたでしょうか？ 


animatecurve コマンドを使うと、曲線を描いていく様子をアニメーションにすることができます。アニメーションを再生するには、図をクリックすると現れるメニュー上の再生ボタンを押します。 

 

例1 y = sin(x) 

> animatecurve(sin(x), x = `+`(`-`(Pi)) .. Pi)
 

 

例2 x = `+`(cos(t), `*`(5, `*`(cos(`+`(`*`(3, `*`(t))))))),  y = `+`(`*`(6, `*`(cos(t))), `-`(`*`(5, `*`(sin(`+`(`*`(3, `*`(t)))))))) 

> animatecurve([`+`(cos(t), `*`(5, `*`(cos(`+`(`*`(3, `*`(t))))))), `+`(`*`(6, `*`(cos(t))), `-`(`*`(5, `*`(sin(`+`(`*`(3, `*`(t)))))))), t = 0 .. `+`(`*`(2, `*`(Pi)))], numpoints = 200)
 

 

ここでは numpoints は曲線を描く際に計算する媒介変数の分割数を 200 に指定しています。 

> animatecurve([cos(t), sin(t), t = 0 .. `+`(`*`(2, `*`(Pi)))])
 

 

逆回り 

> animatecurve([cos(`+`(`-`(t))), sin(`+`(`-`(t))), t = 0 .. `+`(`*`(2, `*`(Pi)))])
 

 

サイクロイド 

> animatecurve([`+`(t, `-`(sin(t))), `+`(1, `-`(cos(t))), t = 0 .. `+`(`*`(2, `*`(Pi)))], scaling = constrained)
 

 

> animatecurve([`+`(cos(t), `*`(5, `*`(cos(`+`(`*`(3, `*`(t))))))), `+`(`*`(6, `*`(cos(t))), `-`(`*`(5, `*`(sin(`+`(`*`(3, `*`(t)))))))), t = 0 .. `+`(`*`(2, `*`(Pi)))], numpoints = 200)
 

 

問題  点が (0,3) を出発して、原点を中心とする半径3の円周上を反時計回りに動くアニメーションを作ってみて下さい。 

問題  x = (`+`(cos(t), `*`(5, `*`(cos(`+`(`*`(3, `*`(t))))))), y = `+`(`*`(6, `*`(cos(t))), `-`(`*`(5, `*`(sin(`+`(`*`(3, `*`(t))))))))) で与えられる曲線を animatecurve を用いて描いてみて下さい。 

numpoints を増やした方がよいでしょう。  

 

3次元のアニメーションは animate の代わりに animate3d を使って同様に描くことができます。 

> animate3d(`*`(sin(`*`(a, `*`(x))), `*`(sin(`*`(a, `*`(y))))), x = 0 .. `+`(`*`(2, `*`(Pi))), y = 0 .. `+`(`*`(2, `*`(Pi))), a = 1 .. 2); 1
 

Plot
 

 

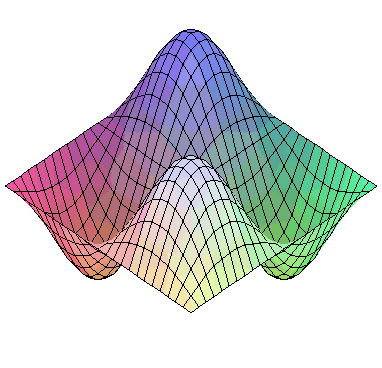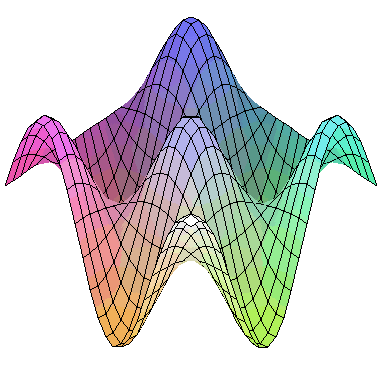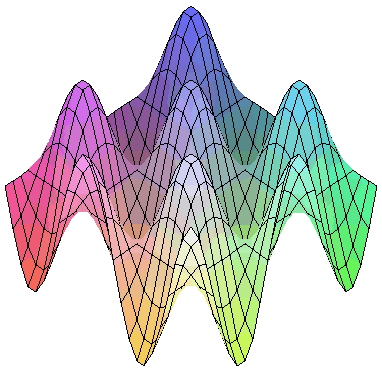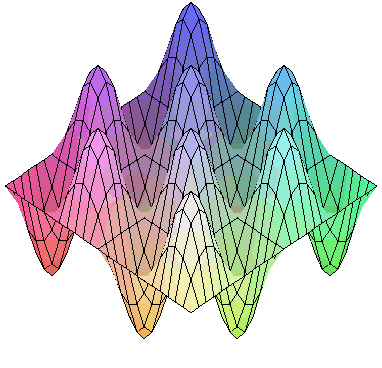別の例 

> animate3d(sin(`*`(x, `*`(y, `*`(a)))), x = -2 .. 2, y = -2 .. 2, a = 0 .. 1, style = patchnogrid, shading = zgrayscale, orientation = [0, 0])
animate3d(sin(`*`(x, `*`(y, `*`(a)))), x = -2 .. 2, y = -2 .. 2, a = 0 .. 1, style = patchnogrid, shading = zgrayscale, orientation = [0, 0])
 

 

参考文献

Maple7 ラーニングガイド，シュプリンガー・フェアラーク東京，2002. 

示野信一，Maple V で見る数学ワールド，シュプリンガー・フェアラーク東京，1999.