フィボナッチ数のプログラム方法は色々なプログラム言語の入門段階でよく例として取り上げられている。
前半は伝統的なプログラム言語でよくやられる方法の Maple 版、
後半は Maple や数式処理ソフトウエア特有の機能を用いてフィボナッチ数を求める方法を紹介する。
フィボナッチ数は数学的に興味深い対象だがここでは数学面には深入りしない。
フィボナッチ数とは 0, 1, 1, 2, 3, 5, 8, 13, ... という数列に現れる数で、この数列は初期条件を
![f[0] = 0, f[1] = 1](images/fibonacci1.gif) として以下
として以下
![f[2] = f[0]+f[1]](images/fibonacci2.gif) のように隣り合う2つのフィボナッチ数を足したものが次のフィボナッチ数になるという規則で定められている。この規則を再帰関係式(漸化式)で書くと、
のように隣り合う2つのフィボナッチ数を足したものが次のフィボナッチ数になるという規則で定められている。この規則を再帰関係式(漸化式)で書くと、
![f[n] = f[n-1]+f[n-2]](images/fibonacci3.gif) となる。
となる。
初期条件と再帰関係式をそのままプログラムにすると次のようになる。
| > | fib := proc(n) if n<2 then n; else fib(n-1)+fib(n-2); end if; end proc: |
| > | fib(5); |
![]()
この再帰プログラムはプログラミングの初歩において簡単な例としてよく紹介される一方、効率が悪いので避けるべきとも教えられている。実際、fib(5)=fib(4)+fib(3)=(fib(3)+fib(2))+(fib(2)+fib(1))=fib(2)+fib(1)+fib(1)+fib(0)+fib(1)+fib(0)+fib(1)=fib(1)+fib(0)++fib(1)+fib(1)+fib(0)+fib(1)+fib(0)+fib(1) という具合に再帰関係式を繰り返し使ってすべてを fib(0) と fib(1) まで帰着して加えて初めて値が求まる。この方法だと
n
を増やすと計算時間は指数関数的に増大してしまう。
一方、手で普通に計算するときは fib(2)=fib(1)+fib(0) の答えを使って fib(3)=fib(2)+fib(1) を計算、fib(3) と fib(2) の値を使って fib(4)=fib(3)+fib(2) を計算、fib(4) と fib(3) の値を使って fib(5)=fib(4)+fib(3) を計算、というように前に計算した結果を利用するので足し算の回数は少なくなる。前の結果を記憶しておいて、それを利用することで同じ計算を重複して行うことを避け、計算量を減らす方法を動的計画法というそうだ。
そうすると計算量は n の多項式オーダーに抑えられる。
これを Maple で実現する方法をいくつか挙げよう。上の再帰プログラムに option remember を付けると、途中で計算した小さいフィボナッチ数の値を無駄なく再利用して計算するので、計算時間は短くなる。
| > | fib := proc(n) option remember; if n<2 then n; else fib(n-1)+fib(n-2); end if; end proc: |
次のようにすれば使っているコンピュータでの実行時間を知ることもできる。
| > | otime := time(): fib(100); time()-otime; |
![]()
![]()
次のように for ループを使って下から順番にやっていっていくのが伝統的なプログラミング方法だろう。
| > | fib := proc(n) local a, b, c, i; a := 1; b := 1; for i from 2 to n do c := a+b; a := b; b := c; end do; c; end proc: |
1つのフィボナッチ数だけでなく、フィボナッチ数列を並べたものが欲しければ、配列に格納していくのが便利だろう。
| > | F := array(1..20): |
| > | F[1] := 1: F[2] := 1: |
| > | for i from 3 to 20 do F[i] := F[i-1]+F[i-2]; end do: |
| > | F[10]; |
![]()
| > | F; |
![]()
配列は評価しないと成分が表示されない。
| > | eval(F); |
![]()
あるいは、リストに変換しておいた方が後で色々と扱うには便利かも知れない。
| > | F := convert(F,list); |
![]()
色々なプログラミング言語でよく紹介されるフィボナッチ数のプログラミングを Maple でやるとどうなるかを記したが、より Maple 特有の(あるいは Maple らしい)ことも書いておこう。
combinat (組合せ論)パッケージにフィボナッチ数が組み込まれているので、次のように呼び出して使うことができる。
| > | with(combinat): |
| > | fibonacci(20); |
![]()
| > | seq(fibonacci(n), n=0..10); |
![]()
フィボナッチ数の一般項はビネの公式として知られており、Maple の rsolve を使ってこれを求めることができる。
| > | fib := unapply(rsolve({f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2)},f),n); |
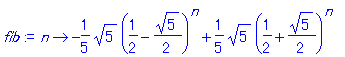
| > | fib(5); |
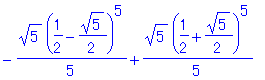
ビネの公式は根号を含むが、簡単にすると自然数になる。
| > | simplify(%); |
![]()
今の場合 expand を使って展開しても望む結果が得られる。
(分母に根号を含む式の場合、simplify では望む結果が得られないこともある
(古いバージョンの Maple)。
その場合は、rationalize や radnormal など有理化の命令が有効である。)
| > | rationalize(fib(10)); |
![]()
一斉に簡単化することもできる。
| > | simplify([seq(fib(n), n=0..10)]); |
![]()
| > | simplify(fib(100)); |
![]()
ビネの公式は黄金比
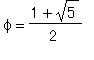 を用いて
を用いて
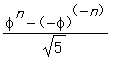 と書けるが、
と書けるが、
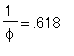 だから
だから
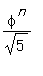 に一番近い整数が
n
番目のフィボナッチ数である。
に一番近い整数が
n
番目のフィボナッチ数である。
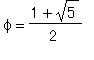 を用いて
を用いて
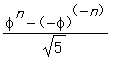 と書けるが、
と書けるが、
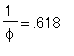 だから
だから
| > | round(evalf(((1+sqrt(5))/2)^100/sqrt(5),50)); |
![]()
計算を高速化するには
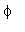 と
と
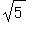 の近似値を用いる必要があるが、
n に応じてどの位の桁数とっておけばよいかを適切に見積もっておかなければいけない。
の近似値を用いる必要があるが、
n に応じてどの位の桁数とっておけばよいかを適切に見積もっておかなければいけない。
Maple 独自の便利なやり方を使いこなすには、option remember, combinat[fibonacci], rsolve, simplify
などをオンラインヘルプを参照する、ウエブ上で検索する、参考書で調べる、人に聞くなどの方法で見つけだす必要がある。
前半で紹介したようなプログラミングができるだけでなく、自分でプログラムを作らなくも色々な数学を扱えるのが Maple や Mathematica, Maxima などの数学ソフトウエアの特徴である。
(5/4/09 修正,4/30/09 作成)