１次元パルス・フーリエ変換・
　　　　NMRスペクトルの測定原理
パルス・フーリエ変換NMR分光器の測定原理を簡単に図示します。下の図に示されたように箱型の分光器において、高周波（６００MHｚ）の電波（ラジオ波）をパルス状（パルス時間幅約１０μｓ）に整形して発生させ、ケーブルを通して超伝導磁石の中央にセットされたタンパク質の入ったサンプル管に照射します。サンプル中のプロトンは超伝導磁石の静止磁場（z軸）を中心として歳差運動していますが、照射したラジオ波の周波数と、歳差運動の周波数（ラーマ周波数）がちょうど一致する（共鳴）とプロトンの核スピンは９０°倒れます。ｘｙ平面上に倒れた核スピンの運動は検出コイルに誘導電流を発生し、FID信号（Free Induction Decay)として観測されます。
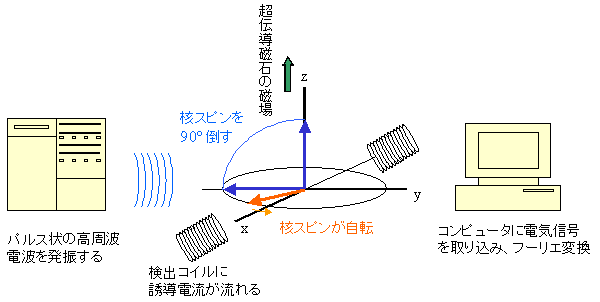
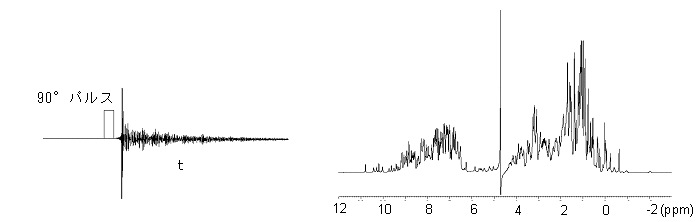
このFID信号はいろいろなラーマ周波数を持ったプロトンの減衰振動波形の重ね合わせになっているので、個々のプロトンのラーマ周波数を知るためにはFID信号の周波数分析をする必要があります。それがFID信号のフーリエ変換という操作です。コンピュータに取り込まれたFID信号はそこで高速フーリエ変換されて、周波数スペクトルを与えます。これがNMRスペクトルと呼ばれるものです。

FID信号

NMRスペクトル

時間軸から周波数軸へのフーリエ変換
２次元NMRスペクトル
　　タンパク質中には非常に沢山のプロトンが存在します。100残基程度のタンパク質でも約700個のプロトンのラーマ周波数を識別する必要があります。1次元のNMRスペクトルでは込み合ってとても識別できません。そこで非常に巧妙な方法を考案したのがR.R.Ernst（1991年ノーベル賞）という人です。第１のパルスで隣接プロトンを90°倒し、第２の90°パルスを照射するまでの待ち時間（展開時間 t1）を色々の長さにとって観測プロトンのFID信号を観測すると、FID信号に隣接プロトンのラーマ周波数とt1時間に依存した振幅変調がかかる結果になるのです（右図参照）。このように、展開時間t１ に応じてFID信号が変化するのは電子スピン結合で相互作用する隣接プロトン間にコヒーレンス移行と呼ばれる現象が起きるからですが、その説明は行列形式の量子力学を必要とするのでここでは省略します。
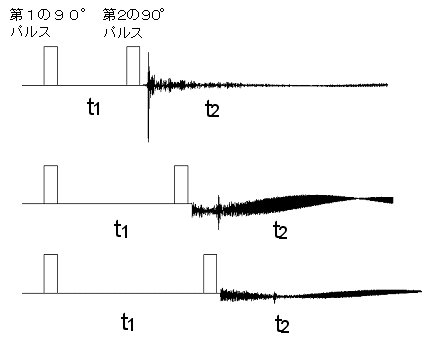
したがってFID信号は展開時間（t1）と観測時間（t2）の2つの時間変数の関数となるので、両方の時間軸でフーリエ変換するとスペクトルは２つの周波数軸ω1、ω2上のピークとして観測されます。これを等高線プロットしたものが左図に示された2次元NMRスペクトルです。左の図はCOSYスペクトルとよばれるもので、隣接する２つのプロトンCαHとNHの交差ピークが現れています。横軸がNH、縦軸がCαH の共鳴周波数を表しています。こうして得られた2次元スペクトルでは、同じ共鳴周波数を持つNHプロトンでも隣接CαHプロトンの共鳴周波数が異なると2次元上では縮退が解けて観測されます。観測プロトンの数が多いタンパク質においては特に重要な性質です。

図をクリックすると拡大します。
さらに、同一残基内に属するCαHとNHの共鳴周波数が一目で分かるために、交差ピークを特定の残基に帰属するために必須のデータとなります。この例はプロトン（１H）という同種核間のコヒーレンス移行を利用したスペクトルでしたが、最近はプロトンと15Nや13C核とのコヒーレンス移行を利用した異種核2次元あるいは3次元NMRスペクトルが測定され、水溶液中におけるタンパク質の構造解析の強力な測定手段となっています。