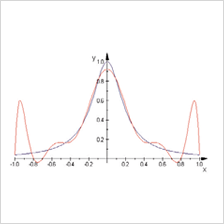
誰もが円周率の近似値3.14を用いて計算した経験があるはず。このように複雑な関数を扱いやすい関数で近似する理論が関数近似理論。

多項式関数、三角関数、指数関数、対数関数などは近似関数として重要です。
関数近似理論により、関数の特性を明らかにします。

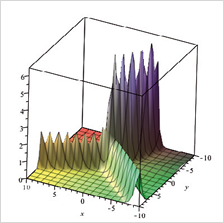
複数の独立変数がある関数、例えば7x yやsin（5x+3y）などをxで微分したりyで微分したりできます。

こうしてできた導関数の間の関係式について調べています。意外なことに、複素数に関する知識が大変役立ちます。
最近は物理に近いテーマに関心があります。

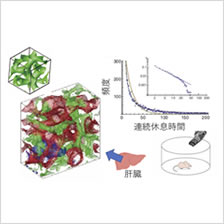
秩序や構造が自然にできあがる不思議な現象である自己組織化現象を対象として、様々な実験を行い、データ解析を行っています。
肝臓のミクロパターンなどの生命現象や化学反応でできるパターンなど、その形成メカニズムを数理的に推定する研究を行っています。

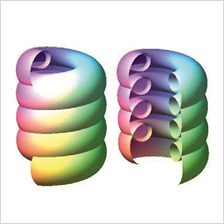
微分幾何学は、微分積分などを使って図形の性質を研究する分野です。

幾何の感覚を取り入れた微分積分の発展形という面もあり、物理学や工学にも応用されます。本研究室では、いろいろな空間内の曲線・曲面の幾何とその応用をテーマに研究を進めています。

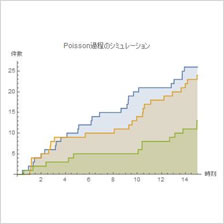
特に確率過程を中心に研究を行っています。確率過程は、時間と共にランダムに変動する現象の数理モデルで、ランダムウォークはその代表です。
確率過程の数理的研究は、工学，物理学，生物学，金融や保険など極めて広範な領域において応用されています。

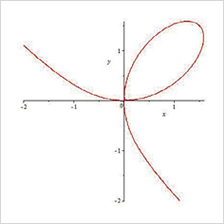
図形の性質を調べる数学分野である幾何学は、測量や天体の運行を調べるために始まり、現代でも科学技術の基礎である数理科学の一分野として発展を続けています。

数学独自の領域においても、時にはコンピュータを駆使して、教育と研究を行っています。

（複素）アフィン空間をはじめとする代数多様体について研究しています。
n次元アフィン空間とは、各点がn個の複素数の組で表される空間で、1次元なら直線、2次元なら平面となります。
代数多様体を、対称性に代表される群の作用という観点から研究しています。

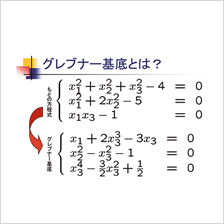
多項式の集まりの中で、特に良い性質を持つ「グレブナー基底」の研究をしています。

キーワードの一つは、多項式の割り算。基本的な応用として、連立方程式の変数消去があり、他にも様々な分野に応用可能なため、多くの数式処理ソフトウエアに実装されています。

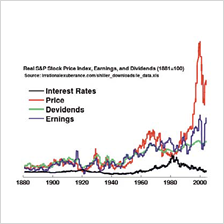
例えばスーパーの野菜や肉などの生鮮食料品の値段は毎日のように変動し、ハンバーガーや牛丼の値段も時々安くなったり高くなったりします。

このような値段の動きがでたらめに上下するのではなく、何らかの規則性を持っているかどうかを統計的に調べます。

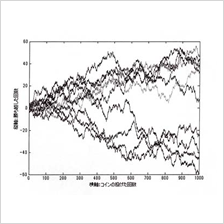
確率論を研究しています。偶然性の中にひそむ法則を数理的に研究する分野です。

例えば、コインを投げ続けると表が出る頻度は2分の1に近づいていきます。
最近は、偶然性とは直接関係のない問題を、偶然性が持つ法則を用いて解決することに興味を持っています。

自然界には、雪の結晶やハチの巣のように秩序ある形が自発的に生み出される現象が数多くあります。

こうした現象を数理モデルを用いて説明する研究が、近年盛んで、研究室では、そこに現れる普遍的な数理構造を抽出したり、解析手法を開発したりしています。